Librerías requeridas: dplyr, flextable, tidyr, ggplot2, DoE.base1 Impacto de la eliminación de réplicas y puntos centrales en diseños factoriales completos \(2^k\)
El presente documento corresponde a un apartado del trabajo titulado “Guía para la implementación de diseños experimentales en la industria farmacéutica”, presentado por Nathalia Cortés Duque como requisito para optar al título de Magíster en Ciencias - Estadística de la Universidad Nacional de Colombia.
2 Objetivo
El presente estudio tiene como propósito analizar el impacto de eliminar réplicas o los puntos centrales en un diseño factorial completo \(2^k\) sobre la significancia estadística de los efectos principales e interacciones, así como sobre el error cuadrático medio (ECM).
3 Metodología
3.1 Evaluación de la significancia de los efectos
Para este fin se realizaron 1000 simulaciones independientes, en las cuales se conocían previamente los efectos significativos de los factores seleccionados aleatoriamente.
En cada simulación se genera un vector con todos los factores e interacciones del respectivo diseño factorial completo \(2^k\) los cuales se agrupan en el vector todos_efectos, así:
| Diseño factorial | Número de efectos | Efectos |
|---|---|---|
| \(2^2\) | 3 | A, B, AB |
| \(2^3\) | 7 | A, B, C, AB, AC, BC, ABC |
| \(2^4\) | 15 | A, B, C, D, AB, AC, AD, BC, BD, CD, ABC, ABD, ACD, BCD, ABCD |
| \(2^5\) | 31 | A, B, C, D, E, AB, AC, AD, AE, BC, BD, BE, CD, CE, DE, ABC, ABD, ABE, ACD, ACE, ADE, BCD, BCE, BDE, CDE, ABCD, ABCE, ABDE, ACDE, BCDE, ABCDE |
A partir de este conjunto, se selecciona aleatoriamente un número de efectos que serán considerados significativos; dichos efectos se denominan . A estos efectos se les asigna un valor aleatorio tomado de una distribución uniforme en el intervalo \(\left[-7,-0.5\right]\) y \(\left[0.5, 7\right]\), mientras que los demás mantienen valor cero. De esta forma se construye el vector , que refleja cuáles efectos son diferentes de cero.
Posteriormente, se clasifica cada efecto como 1 (significativo) o 0 (no significativo) y se almacena en la tabla .
Se genera un diseño factorial \(2^k\) con dos réplicas y cinco puntos centrales (dis1_cod). A este diseño se le asigna una respuesta (yrta) calculada en función de los efectos previamente definidos, es decir, se multiplican los valores de los factores y sus interacciones por los coeficientes correspondientes en efectos_reales_vec, más un término de error aleatorio error con distribución normal \((\mu = 0, \sigma^2 = 2^2)\). Como resultado, los factores seleccionados como activos aportan un efecto distinto de cero, mientras que los demás se anulan. La respuesta final se obtiene sumando estos efectos y el error a una constante de 50.
Este diseño inicial se emplea para construir otras tres variantes eliminando, de manera aleatoria, filas correspondientes a réplicas o puntos centrales: - Diseño con réplicas pero sin puntos centrales (dis2_cod) - Diseño sin réplicas y con cinco puntos centrales (dis3_cod) - Diseño sin réplicas con dos puntos centrales (dis4_cod)
Para cada diseño se ajusta el modelo completo (mod1 <- lm(yrta~A*B, data=dis1_cod)), considerando tanto los efectos principales como las interacciones, así:
Diseño factorial completo \(2^2\):
\[ Y \;=\; \beta_0 \;+\; \beta_1 X_1 \;+\; \beta_2 X_2 \;+\; \beta_{12}X_1X_2 \;+\; \varepsilon, \quad \varepsilon \sim \mathcal{N}(\mu = 0, \sigma^2 = 2^2) \]
Diseño factorial completo \(2^3\):
\[ Y = \beta_0 + \sum_{i=1}^{3} \beta_i X_i + \sum_{i<j}^{3} \beta_{ij} X_i X_j + \beta_{123} X_1 X_2 X_3 + \varepsilon, \quad i = 1,2,3;\;\; j = 1,2,3; \quad \varepsilon \sim N(\mu = 0, \sigma^2 = 2^2) \]
Diseño factorial completo \(2^4\):
\[ Y = \beta_0 + \sum_{i=1}^{4} \beta_i X_i + \sum_{i<j}^{4} \beta_{ij} X_i X_j + \sum_{i<j<k}^{4} \beta_{ijk} X_i X_j X_k + \beta_{1234}\, X_1 X_2 X_3 X_4 + \varepsilon \]
donde,
\[ i,j,k \in \{1,2,3,4\},\;\; \varepsilon \sim \mathcal{N}(\mu = 0, \sigma^2 = 2^2) \]
Diseño factorial completo \(2^5\):
\[ Y = \beta_0 + \sum_{i=1}^{5} \beta_i X_i + \sum_{i<j}^{5} \beta_{ij} X_i X_j + \sum_{i<j<k}^{5} \beta_{ijk} X_i X_j X_k + \sum_{i<j<k<l}^{5} \beta_{ijkl} X_i X_j X_k X_l + \beta_{12345}\, X_1 X_2 X_3 X_4 X_5 + \varepsilon \]
donde,
\[ i,j,k,l \in \{1,2,3,4,5\},\;\; \varepsilon \sim \mathcal{N}(\mu = 0, \sigma^2 = 2^2) \]
Luego, se calcula el ANOVA correspondiente a cada modelo. Los resultados de significancia de los factores y sus interacciones determinados por cada diseño experimental se almacenan en las tablas TAB1, TAB2, TAB3 y TAB4, donde el valor 1 indica significancia estadística (\(p < 0.05\)) y 0 indica no significancia.
Las tablas obtenidos a partir de cada diseño experimental se comparan con la tabla efectos_reales y se calculan los siguientes aspectos: - Concordancia (%): Porcentaje de concordancia entre la significancia real de cada efecto y los detectados por cada diseño. - Potencia (%): Porcentaje de efectos verdaderamente significativos y correctamente identificados como tal por el diseño experimental. - Error tipo I: Proporción de efectos no significativos detectados como significativos por el diseño experimental.
3.2 Evaluación del ECM
Con relación a la evaluación del ECM, se utiliza la metodología de medidas repetidas, en la cual a una misma unidad experimental se le aplican sucesivamente varios tratamientos, generando valores repetidos de la respuesta sobre el mismo individuo (Dı́az Monroy y Mario Alfonso (2012)).
En este estudio, a partir de los diseños simulados en la sección anterior, cada fila corresponde a la simulación del diseño experimental de referencia (dis1_cod), al que se le generan variantes al eliminar réplicas o puntos centrales (dis2_cod, dis3_cod, dis4_cod). Para cada diseño se obtiene como variable respuesta el Error Cuadrático Medio (ECM), calculado mediante la siguiente fórmula:
\[ \text{ECM} = \frac{\text{deviance}(modelo)}{\text{grados de libertad del residual}(modelo)}. \]
Estos resultados fueron compilados en la matriz ECM_tab, que corresponde a la matriz \(X = (x_{ij})\), donde \(x_{ij}\) representa la respuesta del \(i\)-ésimo sujeto al \(j\)-ésimo tratamiento. Incialmente, se realiza un análisis descriptivo de los ECM (Ver Figura 12.1). La matriz \(C\) se utiliza para transformar los datos: \(Y = CX\). De esta forma, el problema se reduce a \((p-1)\) dimensiones y se trabaja con contrastes independientes, evitando dependencia entre medias y permitiendo aplicar la prueba \(T^2\) de Hotelling.
El cálculo implementado en el código sigue la formulación teórica:
\[ T^2 = n(C \overline{X})' (CSC')^{-1} (C \overline{X}), \]
donde \(n\) es el número de simulaciones y \(S\) la matriz de covarianzas estimada mediante
\[ S = \frac{1}{n-1}X'(I - \tfrac{1}{n}\mathbf{1}\mathbf{1}')X. \]
La decisión es rechazar \(H_0\) si, para un nivel de significancia \(\alpha = 0.05\),
\[ F = \frac{n - p + 1}{(n-1)(p-1)} T^2 > F_{(\alpha, p-1, n-p+1)} \]
Luego, se construye la matriz de contrastes \(C\), donde cada fila representa una hipótesis a evaluar. En este caso, se plantea la utilización de una matriz de contrastes \(C_1\) cuyo objetivo es contrastar simultáneamente todas las medias de los tratamientos. Con ello, se busca determinar si existe al menos un tratamiento que difiera significativamente de los demás, lo que constituye el análogo a la prueba ANOVA clásica, pero en un contexto donde los tratamientos son dependientes.
\[ C_1 = \begin{bmatrix} -1 & 1 & 0 & 0 \\ 0 & -1 & 1 & 0 \\ 0 & 0 & -1 & 1 \end{bmatrix} \]
Asimismo, en caso de rechazarse la hipótesis nula en los contrastes previos, resulta pertinente plantear una segunda matriz de contrastes generales de interés \(C_2\), que incluya, por ejemplo, los siguientes contrastes:
\[ C_2 = \begin{bmatrix} -1 & -1 & 1 & 1 \\ 1 & -1 & 0 & 0 \end{bmatrix} \]
Donde los contrastes a evaluar son:
Contraste 1: Contraste que relaciona los diseños con réplica con respecto a los diseños sin réplica \(C_1 =\) (-1, -1, 1, 1)
Contraste 2: Contraste que relaciona el impacto de la réplica en diseños con la misma cantidad de puntos centrales \(C_2 =\) (1, -1, 0, 0)
4 Código
4.1 Diseño \(2^2\)
4.1.1 Significancia de los efectos
Código
# Matrices
TAB1_22 <- matrix(0, nrow = n, ncol = 3)
TAB2_22 <- matrix(0, nrow = n, ncol = 3)
TAB3_22 <- matrix(0, nrow = n, ncol = 3)
TAB4_22 <- matrix(0, nrow = n, ncol = 3)
TAB6_22 <- matrix(0, nrow = n, ncol = 3)
efectos_reales_22 <- matrix(NA, nrow = n, ncol = 3)
names_22 <- c("A","B", "A:B")
colnames(TAB1_22) <- names_22
colnames(TAB2_22) <- names_22
colnames(TAB3_22) <- names_22
colnames(TAB4_22) <- names_22
colnames(TAB6_22) <- names_22
colnames(efectos_reales_22) <- names_22
# Tabla para completar los errores
ECM_tab_22 <- data.frame(
dis1_22 = numeric(n),
dis2_22 = numeric(n),
dis3_22 = numeric(n),
dis4_22 = numeric(n))
# Bucle principal
set.seed(3)
for(i in seq_len(n)){
## Efectos a evaluar en el este diseño
todos_efectos_22 <- c("A", "B", "A:B")
# Selección de un número aleatorio entre 1 y 3
# dado que existen 3 efectos posibles a evaluar en este diseño.
n_ef <- sample(0:length(todos_efectos_22), 1)
# Elección aleatoria _n_ef_ efectos que serán los efectos significativos
efectos_activos <- sample(todos_efectos_22, n_ef)
efectos_reales_22_vec <- setNames(rep(0, length(todos_efectos_22)), todos_efectos_22)
# Asignación de un valor aleatorio a los efectos elegidos como significativos:
efectos_reales_22_vec[efectos_activos] <- sample(c(runif(n_ef, -7, -0.5),
runif(n_ef, 0.5, 7)),n_ef)
# Guardar efectos reales como 1/0
efectos_reales_22[i,] <- c(
as.integer(efectos_reales_22_vec["A"] != 0),
as.integer(efectos_reales_22_vec["B"] != 0),
as.integer(efectos_reales_22_vec["A:B"] != 0))
# Generar respuesta
## Diseño con réplicas y con 5 puntos centrales
dis1_cod <- data.frame(
A = c(rep(c(-1,1),2), rep(c(-1,1),2), rep(0,5)),
B = c(rep(c(rep(-1,2), rep(1,2)), 2), rep(0,5)))
n_corridas <- nrow(dis1_cod)
## Generación del error
error <- rnorm(n_corridas, 0, 2) #error ~ (mu = 0, sigma^2 = 2^2)
## Generación de la respuesta
yrta <- 50 +
efectos_reales_22_vec["A"] * dis1_cod$A +
efectos_reales_22_vec["B"] * dis1_cod$B +
efectos_reales_22_vec["A:B"] * dis1_cod$A * dis1_cod$B +
error
## Asignación de la respuesta al dis1_cod
dis1_cod <- cbind(dis1_cod, yrta)
## Diseño con réplicas y sin puntos centrales
dis2_cod <- dis1_cod[-c(9:13),]
## Diseño sin réplica y con cinco puntos centrales
rep1 <- c(1:4)
rep2 <- c(5:8)
seleccion_name <- sample(c("rep1","rep2"),1) #repetición a eliminar
sel <- get(seleccion_name)
dis3_cod <- dis1_cod[-sel,]
## Diseño sin réplica y con dos puntos centrales
rep1 <- c(1:4)
rep2 <- c(5:8)
seleccion_name <- sample(c("rep1","rep2"),1) #repetición a eliminar
sel <- get(seleccion_name)
rep_pc <- sample(c(9:13),3) #punto central a eliminar
dis4_cod <- dis1_cod[-c(sel,rep_pc),]
## Diseño sin réplica y sin puntos centrales
rep1 <- c(1:4, 9:13)
rep2 <- c(5:8, 9:13)
seleccion_name <- sample(c("rep1","rep2"),1) #repetición a eliminar
sel <- get(seleccion_name)
dis6_cod <- dis1_cod[-sel,]
mod6 <- lm(yrta~A*B, data=dis6_cod)
graf <- suppressMessages(halfnormal(mod6, alpha = 0.05, plot=FALSE, method="Lenth"))
signif <- graf$signif
TAB6_22[i, todos_efectos_22 %in% signif] <- 1
# Modelo
## Evaluación del diseño con réplicas y con cinco puntos centrales
mod1 <- lm(yrta~A*B, data=dis1_cod)
## Evaluación del diseño con réplicas y sin puntos centrales
mod2 <- lm(yrta~A*B, data=dis2_cod)
## Evaluación del diseño sin réplicas y con cinco puntos centrales
mod3 <- lm(yrta~A*B, data=dis3_cod)
## Evaluación del diseño sin réplicas y con dos puntos centrales
mod4 <- lm(yrta~A*B, data=dis4_cod)
## Almacenar los ECM
ECM_tab_22$dis1_22[i] <- (deviance(mod1) / df.residual(mod1))
ECM_tab_22$dis2_22[i] <- (deviance(mod2) / df.residual(mod2))
ECM_tab_22$dis3_22[i] <- (deviance(mod3) / df.residual(mod3))
ECM_tab_22$dis4_22[i] <- (deviance(mod4) / df.residual(mod4))
# Lista de modelos y de tablas
mods <- list(mod1, mod2, mod3, mod4)
tabs <- list(TAB1_22, TAB2_22, TAB3_22, TAB4_22)
for (j in seq_along(mods)) {
tabs[[j]][i, ] <- sapply(1:3, function(k) {
as.integer(anova(mods[[j]])[k, 5] <= 0.05) })}
## Evaluación del diseño con réplicas y con cinco puntos centrales
TAB1_22 <- tabs[[1]]
## Evaluación del diseño con réplicas y sin puntos centrales
TAB2_22 <- tabs[[2]]
## Evaluación del diseño sin réplicas y con cinco puntos centrales
TAB3_22 <- tabs[[3]]
## Evaluación del diseño sin réplicas y con dos puntos centrales
TAB4_22 <- tabs[[4]]} 4.1.2 Potencia y error tipo I
Código
## Evaluación del diseño con réplicas y con cinco puntos centrales
comp1_22 <- round(colSums(efectos_reales_22 == TAB1_22) / n * 100, 2)
pot1_22 <- round(colSums((efectos_reales_22 == 1) & (TAB1_22 == 1)) /
colSums(efectos_reales_22 == 1) * 100, 2)
err1_22 <- round(colSums((efectos_reales_22 == 0) & (TAB1_22 == 1)) /
colSums(efectos_reales_22 == 0) * 100, 2)
## Evaluación del diseño con réplicas y sin puntos centrales
comp2_22 <- round(colSums(efectos_reales_22 == TAB2_22) / n * 100, 2)
pot2_22 <- round(colSums((efectos_reales_22 == 1) & (TAB2_22 == 1)) /
colSums(efectos_reales_22 == 1) * 100, 2)
err2_22 <- round(colSums((efectos_reales_22 == 0) & (TAB2_22 == 1)) /
colSums(efectos_reales_22 == 0) * 100, 2)
## Evaluación del diseño sin réplicas y con cinco puntos centrales
comp3_22 <- round(colSums(efectos_reales_22 == TAB3_22) / n * 100, 2)
pot3_22 <- round(colSums((efectos_reales_22 == 1) & (TAB3_22 == 1)) /
colSums(efectos_reales_22 == 1) * 100, 2)
err3_22 <- round(colSums((efectos_reales_22 == 0) & (TAB3_22 == 1)) /
colSums(efectos_reales_22 == 0) * 100, 2)
## Evaluación del diseño sin réplicas y con dos puntos centrales
comp4_22 <- round(colSums(efectos_reales_22 == TAB4_22) / n * 100, 2)
pot4_22 <- round(colSums((efectos_reales_22 == 1) & (TAB4_22 == 1)) /
colSums(efectos_reales_22 == 1) * 100, 2)
err4_22 <- round(colSums((efectos_reales_22 == 0) & (TAB4_22 == 1)) /
colSums(efectos_reales_22 == 0) * 100, 2)
## Evaluación del diseño sin réplica y sin puntos centrales
comp6_22 <- round(colSums(efectos_reales_22 == TAB6_22) / n * 100, 2)
pot6_22 <- round(colSums((efectos_reales_22 == 1) & (TAB6_22 == 1)) /
colSums(efectos_reales_22 == 1) * 100, 2)
err6_22 <- round(colSums((efectos_reales_22 == 0) & (TAB6_22 == 1)) /
colSums(efectos_reales_22 == 0) * 100, 2)4.2 Diseño \(2^3\)
4.2.1 Significancia de los efectos
Código
# Matrices
TAB1_23 <- matrix(0, nrow = n, ncol = 7)
TAB2_23 <- matrix(0, nrow = n, ncol = 7)
TAB3_23 <- matrix(0, nrow = n, ncol = 7)
TAB4_23 <- matrix(0, nrow = n, ncol = 7)
TAB6_23 <- matrix(0, nrow = n, ncol = 7)
efectos_reales_23 <- matrix(0, nrow = n, ncol = 7)
names_23 <- c("A","B","C","A:B","A:C","B:C","A:B:C")
colnames(TAB1_23) <- names_23
colnames(TAB2_23) <- names_23
colnames(TAB3_23) <- names_23
colnames(TAB4_23) <- names_23
colnames(TAB6_23) <- names_23
colnames(efectos_reales_23) <- names_23
# Tabla para completar los errores
ECM_tab_23 <- data.frame(
dis1_23 = numeric(n),
dis2_23 = numeric(n),
dis3_23 = numeric(n),
dis4_23 = numeric(n))
# Bucle principal
set.seed(3)
for(i in seq_len(n)){
## Efectos a evaluar en el este diseño
todos_efectos_23 <- c("A","B","C","A:B","A:C","B:C","A:B:C")
# Selección de un número aleatorio entre 1 y 7
# dado que existen 7 efectos posibles a evaluar en este diseño.
n_ef <- sample(0:length(todos_efectos_23), 1)
# Elección aleatoria _n_ef_ efectos que serán los efectos significativos
efectos_activos <- sample(todos_efectos_23, n_ef)
efectos_reales_23_vec <- setNames(rep(0, length(todos_efectos_23)), todos_efectos_23)
# Asignación de un valor aleatorio a los efectos elegidos como significativos:
efectos_reales_23_vec[efectos_activos] <- sample(c(runif(n_ef, -7, -0.5),
runif(n_ef, 0.5, 7)),n_ef)
# Guardar efectos reales como 1/0
efectos_reales_23[i,] <- c(
as.integer(efectos_reales_23_vec["A"] != 0),
as.integer(efectos_reales_23_vec["B"] != 0),
as.integer(efectos_reales_23_vec["C"] != 0),
as.integer(efectos_reales_23_vec["A:B"] != 0),
as.integer(efectos_reales_23_vec["A:C"] != 0),
as.integer(efectos_reales_23_vec["B:C"] != 0),
as.integer(efectos_reales_23_vec["A:B:C"] != 0))
# Generar respuesta
## Diseño de variables codificadas con réplicas y con 5 puntos centrales
dis1_cod <- data.frame(
A = c(rep(c(-1,1),4), rep(c(-1,1),4), rep(0,5)),
B = c(rep(c(rep(-1,2), rep(1,2)), 4), rep(0,5)),
C = c(rep(-1,4), rep(1,4), rep(-1,4), rep(1,4), rep(0,5)))
n_corridas <- nrow(dis1_cod)
## Generación del error
error <- rnorm(n_corridas, 0, 2) #error ~ (mu = 0, sigma^2 = 2^2)
## Generación de la respuesta
yrta <- 50 +
efectos_reales_23_vec["A"] * dis1_cod$A +
efectos_reales_23_vec["B"] * dis1_cod$B +
efectos_reales_23_vec["C"] * dis1_cod$C +
efectos_reales_23_vec["A:B"] * dis1_cod$A * dis1_cod$B +
efectos_reales_23_vec["A:C"] * dis1_cod$A * dis1_cod$C +
efectos_reales_23_vec["B:C"] * dis1_cod$B * dis1_cod$C +
efectos_reales_23_vec["A:B:C"] * dis1_cod$A * dis1_cod$B * dis1_cod$C +
error
## Asignación de la respuesta al dis1_cod
dis1_cod <- cbind(dis1_cod, yrta)
## Diseño con réplicas y sin puntos centrales
dis2_cod <- dis1_cod[-c(17:21),]
## Diseño sin réplica y con cinco puntos centrales
rep1 <- c(1:8)
rep2 <- c(9:16)
seleccion_name <- sample(c("rep1","rep2"),1) #repetición a eliminar
sel <- get(seleccion_name)
dis3_cod <- dis1_cod[-sel,]
## Diseño sin réplica y con dos puntos centrales
rep1 <- c(1:8)
rep2 <- c(9:16)
seleccion_name <- sample(c("rep1","rep2"),1) #repetición a eliminar
sel <- get(seleccion_name)
rep_pc <- sample(c(17:21),3) #punto central a eliminar
dis4_cod <- dis1_cod[-c(sel,rep_pc),]
## Diseño sin réplica y sin puntos centrales
rep1 <- c(1:8, 17:21)
rep2 <- c(9:16, 17:21)
seleccion_name <- sample(c("rep1","rep2"),1) #repetición a eliminar
sel <- get(seleccion_name)
dis6_cod <- dis1_cod[-sel,]
# Modelo
## Evaluación del diseño con réplicas y con cinco puntos centrales
mod1 <- lm(yrta~A*B*C, data=dis1_cod)
## Evaluación del diseño con réplicas y sin puntos centrales
mod2 <- lm(yrta~A*B*C, data=dis2_cod)
## Evaluación del diseño sin réplicas y con cinco puntos centrales
mod3 <- lm(yrta~A*B*C, data=dis3_cod)
## Evaluación del diseño sin réplicas y con dos puntos centrales
mod4 <- lm(yrta~A*B*C, data=dis4_cod)
## Evaluación del diseño sin réplica y sin puntos centrales
mod6 <- lm(yrta~A*B*C, data=dis6_cod)
# Efectos de acuerdo al gráfico de Lenth
graf <- suppressMessages(halfnormal(mod6, alpha = 0.05, plot=FALSE,
method="Lenth"))
signif <- graf$signif
TAB6_23[i, todos_efectos_23 %in% signif] <- 1
## Almacenar los ECM
ECM_tab_23$dis1_23[i] <- (deviance(mod1) / df.residual(mod1))
ECM_tab_23$dis2_23[i] <- (deviance(mod2) / df.residual(mod2))
ECM_tab_23$dis3_23[i] <- (deviance(mod3) / df.residual(mod3))
ECM_tab_23$dis4_23[i] <- (deviance(mod4) / df.residual(mod4))
# Lista de modelos y de tablas
mods <- list(mod1, mod2, mod3, mod4)
tabs <- list(TAB1_23, TAB2_23, TAB3_23, TAB4_23)
for (j in seq_along(mods)) {
tabs[[j]][i, ] <- sapply(1:7, function(k) {
as.integer(anova(mods[[j]])[k, 5] <= 0.05) })}
## Evaluación del diseño con réplicas y con cinco puntos centrales
TAB1_23 <- tabs[[1]]
## Evaluación del diseño con réplicas y sin puntos centrales
TAB2_23 <- tabs[[2]]
## Evaluación del diseño sin réplicas y con cinco puntos centrales
TAB3_23 <- tabs[[3]]
## Evaluación del diseño sin réplicas y con dos puntos centrales
TAB4_23 <- tabs[[4]]} 4.2.2 Potencia y error tipo I
Código
## Evaluación del diseño con réplicas y con cinco puntos centrales
comp1_23 <- round(colSums(efectos_reales_23 == TAB1_23) / n * 100, 2)
pot1_23 <- round(colSums((efectos_reales_23 == 1) & (TAB1_23 == 1)) /
colSums(efectos_reales_23 == 1) * 100, 2)
err1_23 <- round(colSums((efectos_reales_23 == 0) & (TAB1_23 == 1)) /
colSums(efectos_reales_23 == 0) * 100, 2)
## Evaluación del diseño con réplicas y sin puntos centrales
comp2_23 <- round(colSums(efectos_reales_23 == TAB2_23) / n * 100, 2)
pot2_23 <- round(colSums((efectos_reales_23 == 1) & (TAB2_23 == 1)) /
colSums(efectos_reales_23 == 1) * 100, 2)
err2_23 <- round(colSums((efectos_reales_23 == 0) & (TAB2_23 == 1)) /
colSums(efectos_reales_23 == 0) * 100, 2)
## Evaluación del diseño sin réplicas y con cinco puntos centrales
comp3_23 <- round(colSums(efectos_reales_23 == TAB3_23) / n * 100, 2)
pot3_23 <- round(colSums((efectos_reales_23 == 1) & (TAB3_23 == 1)) /
colSums(efectos_reales_23 == 1) * 100, 2)
err3_23 <- round(colSums((efectos_reales_23 == 0) & (TAB3_23 == 1)) /
colSums(efectos_reales_23 == 0) * 100, 2)
## Evaluación del diseño sin réplicas y con dos puntos centrales
comp4_23 <- round(colSums(efectos_reales_23 == TAB4_23) / n * 100, 2)
pot4_23 <- round(colSums((efectos_reales_23 == 1) & (TAB4_23 == 1)) /
colSums(efectos_reales_23 == 1) * 100, 2)
err4_23 <- round(colSums((efectos_reales_23 == 0) & (TAB4_23 == 1)) /
colSums(efectos_reales_23 == 0) * 100, 2)
## Evaluación del diseño sin réplicas y sin puntos centrales
comp6_23 <- round(colSums(efectos_reales_23 == TAB6_23) / n * 100, 2)
pot6_23 <- round(colSums((efectos_reales_23 == 1) & (TAB6_23 == 1)) /
colSums(efectos_reales_23 == 1) * 100, 2)
err6_23 <- round(colSums((efectos_reales_23 == 0) & (TAB6_23 == 1)) /
colSums(efectos_reales_23 == 0) * 100, 2)4.3 Diseño \(2^4\)
4.3.1 Significancia de los efectos
Código
# Matrices
TAB1_24 <- matrix(0, nrow = n, ncol = 15)
TAB2_24 <- matrix(0, nrow = n, ncol = 15)
TAB3_24 <- matrix(0, nrow = n, ncol = 15)
TAB4_24 <- matrix(0, nrow = n, ncol = 15)
TAB6_24 <- matrix(0, nrow = n, ncol = 15)
efectos_reales_24 <- matrix(0, nrow = n, ncol = 15)
names_24 <- c("A", "B", "C", "D",
"A:B", "A:C", "B:C", "A:D", "B:D", "C:D",
"A:B:C", "A:B:D", "A:C:D", "B:C:D",
"A:B:C:D")
colnames(TAB1_24) <- names_24
colnames(TAB2_24) <- names_24
colnames(TAB3_24) <- names_24
colnames(TAB4_24) <- names_24
colnames(TAB6_24) <- names_24
colnames(efectos_reales_24) <- names_24
# Tabla para completar los errores
ECM_tab_24 <- data.frame(
dis1_24 = numeric(n),
dis2_24 = numeric(n),
dis3_24 = numeric(n),
dis4_24 = numeric(n))
# Bucle principal
set.seed(3)
for(i in seq_len(n)){
## Efectos a evaluar en el este diseño
todos_efectos_24 <- c("A", "B", "C", "D",
"A:B", "A:C", "B:C", "A:D", "B:D", "C:D",
"A:B:C", "A:B:D", "A:C:D", "B:C:D",
"A:B:C:D")
# Selección de un número aleatorio entre 1 y 15
# dado que existen 15 efectos posibles a evaluar en este diseño.
n_ef <- sample(0:length(todos_efectos_24), 1)
# Elección aleatoria _n_ef_ efectos que serán los efectos significativos
efectos_activos <- sample(todos_efectos_24, n_ef)
efectos_reales_24_vec <- setNames(rep(0, length(todos_efectos_24)), todos_efectos_24)
# Asignación de un valor aleatorio a los efectos elegidos como significativos:
efectos_reales_24_vec[efectos_activos] <- sample(c(runif(n_ef, -7, -0.5),
runif(n_ef, 0.5, 7)),n_ef)
# Guardar efectos reales como 1/0
efectos_reales_24[i, ] <- c(
as.integer(efectos_reales_24_vec["A"] != 0),
as.integer(efectos_reales_24_vec["B"] != 0),
as.integer(efectos_reales_24_vec["C"] != 0),
as.integer(efectos_reales_24_vec["D"] != 0),
as.integer(efectos_reales_24_vec["A:B"] != 0),
as.integer(efectos_reales_24_vec["A:C"] != 0),
as.integer(efectos_reales_24_vec["B:C"] != 0),
as.integer(efectos_reales_24_vec["A:D"] != 0),
as.integer(efectos_reales_24_vec["B:D"] != 0),
as.integer(efectos_reales_24_vec["C:D"] != 0),
as.integer(efectos_reales_24_vec["A:B:C"] != 0),
as.integer(efectos_reales_24_vec["A:B:D"] != 0),
as.integer(efectos_reales_24_vec["A:C:D"] != 0),
as.integer(efectos_reales_24_vec["B:C:D"] != 0),
as.integer(efectos_reales_24_vec["A:B:C:D"] != 0))
# Generar respuesta
## Diseño de variables codificadas con réplicas y con 5 puntos centrales
dis1_cod <- data.frame(
A = c(rep(c(-1,1), 8), rep(c(-1,1), 8), rep(0,5)),
B = c(rep(c(rep(-1,2), rep(1,2)), 4),
rep(c(rep(-1,2), rep(1,2)), 4),
rep(0,5)),
C = c(rep(c(rep(-1,4), rep(1,4)), 2),
rep(c(rep(-1,4), rep(1,4)), 2),
rep(0,5)),
D = c(rep(-1,8), rep(1,8),
rep(-1,8), rep(1,8),
rep(0,5)))
n_corridas <- nrow(dis1_cod)
## Generación del error
error <- rnorm(n_corridas, 0, 2) #error ~ (mu = 0, sigma^2 = 2^2)
## Generación de la respuesta
yrta <- 50 +
efectos_reales_24_vec["A"] * dis1_cod$A +
efectos_reales_24_vec["B"] * dis1_cod$B +
efectos_reales_24_vec["C"] * dis1_cod$C +
efectos_reales_24_vec["D"] * dis1_cod$D +
efectos_reales_24_vec["A:B"] * dis1_cod$A * dis1_cod$B +
efectos_reales_24_vec["A:C"] * dis1_cod$A * dis1_cod$C +
efectos_reales_24_vec["B:C"] * dis1_cod$B * dis1_cod$C +
efectos_reales_24_vec["A:D"] * dis1_cod$A * dis1_cod$D +
efectos_reales_24_vec["B:D"] * dis1_cod$B * dis1_cod$D +
efectos_reales_24_vec["C:D"] * dis1_cod$C * dis1_cod$D +
efectos_reales_24_vec["A:B:C"] * dis1_cod$A * dis1_cod$B * dis1_cod$C +
efectos_reales_24_vec["A:B:D"] * dis1_cod$A * dis1_cod$B * dis1_cod$D +
efectos_reales_24_vec["A:C:D"] * dis1_cod$A * dis1_cod$C * dis1_cod$D +
efectos_reales_24_vec["B:C:D"] * dis1_cod$B * dis1_cod$C * dis1_cod$D +
efectos_reales_24_vec["A:B:C:D"] * dis1_cod$A * dis1_cod$B * dis1_cod$C * dis1_cod$D +
error
## Asignación de la respuesta al dis1_cod
dis1_cod <- cbind(dis1_cod, yrta)
## Diseño con réplicas y sin puntos centrales
dis2_cod <- dis1_cod[-c(33:37),]
## Diseño sin réplica y con cinco puntos centrales
rep1 <- c(1:16)
rep2 <- c(17:32)
seleccion_name <- sample(c("rep1","rep2"),1) #repetición a eliminar
sel <- get(seleccion_name)
dis3_cod <- dis1_cod[-sel,]
## Diseño sin réplica y con dos puntos centrales
rep1 <- c(1:16)
rep2 <- c(17:32)
seleccion_name <- sample(c("rep1","rep2"),1) #repetición a eliminar
sel <- get(seleccion_name)
rep_pc <- sample(c(33:37),3) #punto central a eliminar
dis4_cod <- dis1_cod[-c(sel,rep_pc),]
## Diseño sin réplica y sin puntos centrales
rep1 <- c(1:16, 33:37)
rep2 <- c(17:32, 33:37)
seleccion_name <- sample(c("rep1","rep2"),1) #repetición a eliminar
sel <- get(seleccion_name)
dis6_cod <- dis1_cod[-sel,]
mod6 <- lm(yrta~A*B*C*D, data=dis6_cod)
graf <- suppressMessages(halfnormal(mod6, alpha = 0.05, plot=FALSE, method="Lenth"))
signif <- graf$signif
TAB6_24[i, todos_efectos_24 %in% signif] <- 1
# Modelo
## Evaluación del diseño con réplicas y con cinco puntos centrales
mod1 <- lm(yrta~A*B*C*D, data=dis1_cod)
## Evaluación del diseño con réplicas y sin puntos centrales
mod2 <- lm(yrta~A*B*C*D, data=dis2_cod)
## Evaluación del diseño sin réplicas y con cinco puntos centrales
mod3 <- lm(yrta~A*B*C*D, data=dis3_cod)
## Evaluación del diseño sin réplicas y con dos puntos centrales
mod4 <- lm(yrta~A*B*C*D, data=dis4_cod)
## Almacenar los ECM
ECM_tab_24$dis1_24[i] <- (deviance(mod1) / df.residual(mod1))
ECM_tab_24$dis2_24[i] <- (deviance(mod2) / df.residual(mod2))
ECM_tab_24$dis3_24[i] <- (deviance(mod3) / df.residual(mod3))
ECM_tab_24$dis4_24[i] <- (deviance(mod4) / df.residual(mod4))
# Lista de modelos y de tablas
mods <- list(mod1, mod2, mod3, mod4)
tabs <- list(TAB1_24, TAB2_24, TAB3_24, TAB4_24)
for (j in seq_along(mods)) {
tabs[[j]][i, ] <- sapply(1:15, function(k) {
as.integer(anova(mods[[j]])[k, 5] <= 0.05) })}
## Diseño con réplicas y con cinco puntos centrales
TAB1_24 <- tabs[[1]]
## Evaluación del diseño con réplicas y sin puntos centrales
TAB2_24 <- tabs[[2]]
## Evaluación del diseño sin réplicas y con cinco puntos centrales
TAB3_24 <- tabs[[3]]
## Evaluación del diseño sin réplicas y con dos puntos centrales
TAB4_24 <- tabs[[4]]} 4.3.2 Potencia y error tipo I
Código
## Evaluación del diseño con réplicas y con cinco puntos centrales
comp1_24 <- round(colSums(efectos_reales_24 == TAB1_24) / n * 100, 2)
pot1_24 <- round(colSums((efectos_reales_24 == 1) & (TAB1_24 == 1)) /
colSums(efectos_reales_24 == 1) * 100, 2)
err1_24 <- round(colSums((efectos_reales_24 == 0) & (TAB1_24 == 1)) /
colSums(efectos_reales_24 == 0) * 100, 2)
## Evaluación del diseño con réplicas y sin puntos centrales
comp2_24 <- round(colSums(efectos_reales_24 == TAB2_24) / n * 100, 2)
pot2_24 <- round(colSums((efectos_reales_24 == 1) & (TAB2_24 == 1)) /
colSums(efectos_reales_24 == 1) * 100, 2)
err2_24 <- round(colSums((efectos_reales_24 == 0) & (TAB2_24 == 1)) /
colSums(efectos_reales_24 == 0) * 100, 2)
## Evaluación del diseño sin réplicas y con cinco puntos centrales
comp3_24 <- round(colSums(efectos_reales_24 == TAB3_24) / n * 100, 2)
pot3_24 <- round(colSums((efectos_reales_24 == 1) & (TAB3_24 == 1)) /
colSums(efectos_reales_24 == 1) * 100, 2)
err3_24 <- round(colSums((efectos_reales_24 == 0) & (TAB3_24 == 1)) /
colSums(efectos_reales_24 == 0) * 100, 2)
## Evaluación del diseño sin réplicas y con dos puntos centrales
comp4_24 <- round(colSums(efectos_reales_24 == TAB4_24) / n * 100, 2)
pot4_24 <- round(colSums((efectos_reales_24 == 1) & (TAB4_24 == 1)) /
colSums(efectos_reales_24 == 1) * 100, 2)
err4_24 <- round(colSums((efectos_reales_24 == 0) & (TAB4_24 == 1)) /
colSums(efectos_reales_24 == 0) * 100, 2)
## Evaluación del diseño sin réplicas y sin puntos centrales
comp6_24 <- round(colSums(efectos_reales_24 == TAB6_24) / n * 100, 2)
pot6_24 <- round(colSums((efectos_reales_24 == 1) & (TAB6_24 == 1)) /
colSums(efectos_reales_24 == 1) * 100, 2)
err6_24 <- round(colSums((efectos_reales_24 == 0) & (TAB6_24 == 1)) /
colSums(efectos_reales_24 == 0) * 100, 2)4.4 Diseño \(2^5\)
4.4.1 Significancia de los efectos
Código
# Matrices
TAB1_25 <- matrix(NA, nrow = n, ncol = 31)
TAB2_25 <- matrix(NA, nrow = n, ncol = 31)
TAB3_25 <- matrix(NA, nrow = n, ncol = 31)
TAB4_25 <- matrix(NA, nrow = n, ncol = 31)
TAB6_25 <- matrix(0, nrow = n, ncol = 31)
efectos_reales_25 <- matrix(0, nrow = n, ncol = 31)
names_25 <- c("A","B","C","D","E",
"A:B","A:C","B:C","A:D","B:D","C:D","A:E","B:E","C:E","D:E",
"A:B:C","A:B:D","A:C:D","B:C:D","A:B:E","A:C:E","B:C:E","A:D:E","B:D:E","C:D:E",
"A:B:C:D","A:B:C:E","A:B:D:E","A:C:D:E","B:C:D:E",
"A:B:C:D:E")
colnames(TAB1_25) <- names_25
colnames(TAB2_25) <- names_25
colnames(TAB3_25) <- names_25
colnames(TAB4_25) <- names_25
colnames(TAB6_25) <- names_25
colnames(efectos_reales_25) <- names_25
# Tabla para completar los errores
ECM_tab_25 <- data.frame(
dis1_25 = numeric(n),
dis2_25 = numeric(n),
dis3_25 = numeric(n),
dis4_25 = numeric(n))
# Bucle principal
set.seed(3)
for(i in seq_len(n)){
## Efectos a evaluar en el este diseño
todos_efectos_25 <- c("A","B","C","D","E",
"A:B","A:C","B:C","A:D","B:D","C:D","A:E","B:E","C:E","D:E",
"A:B:C","A:B:D","A:C:D","B:C:D","A:B:E","A:C:E","B:C:E","A:D:E","B:D:E","C:D:E",
"A:B:C:D","A:B:C:E","A:B:D:E","A:C:D:E","B:C:D:E",
"A:B:C:D:E")
# Selección de un número aleatorio entre 1 y 31
# dado que existen 31 efectos posibles a evaluar en este diseño.
n_ef <- sample(0:length(todos_efectos_25), 1)
# Elección aleatoria _n_ef_ efectos que serán los efectos significativos
efectos_activos <- sample(todos_efectos_25, n_ef)
efectos_reales_25_vec <- setNames(rep(0, length(todos_efectos_25)), todos_efectos_25)
# Asignación de un valor aleatorio a los efectos elegidos como significativos:
efectos_reales_25_vec[efectos_activos] <- sample(c(runif(n_ef, -7, -0.5),
runif(n_ef, 0.5, 7)),n_ef)
# Guardar efectos reales como 1/0
efectos_reales_25[i, ] <- c(
as.integer(efectos_reales_25_vec["A"] != 0),
as.integer(efectos_reales_25_vec["B"] != 0),
as.integer(efectos_reales_25_vec["C"] != 0),
as.integer(efectos_reales_25_vec["D"] != 0),
as.integer(efectos_reales_25_vec["E"] != 0),
as.integer(efectos_reales_25_vec["A:B"] != 0),
as.integer(efectos_reales_25_vec["A:C"] != 0),
as.integer(efectos_reales_25_vec["B:C"] != 0),
as.integer(efectos_reales_25_vec["A:D"] != 0),
as.integer(efectos_reales_25_vec["B:D"] != 0),
as.integer(efectos_reales_25_vec["C:D"] != 0),
as.integer(efectos_reales_25_vec["A:E"] != 0),
as.integer(efectos_reales_25_vec["B:E"] != 0),
as.integer(efectos_reales_25_vec["C:E"] != 0),
as.integer(efectos_reales_25_vec["D:E"] != 0),
as.integer(efectos_reales_25_vec["A:B:C"] != 0),
as.integer(efectos_reales_25_vec["A:B:D"] != 0),
as.integer(efectos_reales_25_vec["A:C:D"] != 0),
as.integer(efectos_reales_25_vec["B:C:D"] != 0),
as.integer(efectos_reales_25_vec["A:B:E"] != 0),
as.integer(efectos_reales_25_vec["A:C:E"] != 0),
as.integer(efectos_reales_25_vec["B:C:E"] != 0),
as.integer(efectos_reales_25_vec["A:D:E"] != 0),
as.integer(efectos_reales_25_vec["B:D:E"] != 0),
as.integer(efectos_reales_25_vec["C:D:E"] != 0),
as.integer(efectos_reales_25_vec["A:B:C:D"] != 0),
as.integer(efectos_reales_25_vec["A:B:C:E"] != 0),
as.integer(efectos_reales_25_vec["A:B:D:E"] != 0),
as.integer(efectos_reales_25_vec["A:C:D:E"] != 0),
as.integer(efectos_reales_25_vec["B:C:D:E"] != 0),
as.integer(efectos_reales_25_vec["A:B:C:D:E"]!= 0))
# Generar respuesta
## Diseño de variables codificadas con réplicas y con 5 puntos centrales
dis1_cod <- data.frame(
A = c(rep(c(-1,1),16), rep(c(-1,1),16), rep(0,5)),
B = c(rep(c(rep(-1,2), rep(1,2)),8), rep(c(rep(-1,2), rep(1,2)),8),rep(0,5)),
C = c(rep(c(rep(-1,4), rep(1,4)),4), rep(c(rep(-1,4), rep(1,4)),4),rep(0,5)),
D = c(rep(c(rep(-1,8), rep(1,8)),2), rep(c(rep(-1,8), rep(1,8)),2),rep(0,5)),
E = c(rep(-1,16), rep(1,16), rep(-1,16), rep(1,16), rep(0,5)))
n_corridas <- nrow(dis1_cod)
## Generación del error
error <- rnorm(n_corridas, 0, 2) #error ~ (mu = 0, sigma^2 = 2^2)
## Generación de la respuesta
yrta <- 50 +
efectos_reales_25_vec["A"] * dis1_cod$A +
efectos_reales_25_vec["B"] * dis1_cod$B +
efectos_reales_25_vec["C"] * dis1_cod$C +
efectos_reales_25_vec["D"] * dis1_cod$D +
efectos_reales_25_vec["E"] * dis1_cod$E +
efectos_reales_25_vec["A:B"] * dis1_cod$A * dis1_cod$B +
efectos_reales_25_vec["A:C"] * dis1_cod$A * dis1_cod$C +
efectos_reales_25_vec["B:C"] * dis1_cod$B * dis1_cod$C +
efectos_reales_25_vec["A:D"] * dis1_cod$A * dis1_cod$D +
efectos_reales_25_vec["B:D"] * dis1_cod$B * dis1_cod$D +
efectos_reales_25_vec["C:D"] * dis1_cod$C * dis1_cod$D +
efectos_reales_25_vec["A:E"] * dis1_cod$A * dis1_cod$E +
efectos_reales_25_vec["B:E"] * dis1_cod$B * dis1_cod$E +
efectos_reales_25_vec["C:E"] * dis1_cod$C * dis1_cod$E +
efectos_reales_25_vec["D:E"] * dis1_cod$D * dis1_cod$E +
efectos_reales_25_vec["A:B:C"] * dis1_cod$A * dis1_cod$B * dis1_cod$C +
efectos_reales_25_vec["A:B:D"] * dis1_cod$A * dis1_cod$B * dis1_cod$D +
efectos_reales_25_vec["A:C:D"] * dis1_cod$A * dis1_cod$C * dis1_cod$D +
efectos_reales_25_vec["B:C:D"] * dis1_cod$B * dis1_cod$C * dis1_cod$D +
efectos_reales_25_vec["A:B:E"] * dis1_cod$A * dis1_cod$B * dis1_cod$E +
efectos_reales_25_vec["A:C:E"] * dis1_cod$A * dis1_cod$C * dis1_cod$E +
efectos_reales_25_vec["B:C:E"] * dis1_cod$B * dis1_cod$C * dis1_cod$E +
efectos_reales_25_vec["A:D:E"] * dis1_cod$A * dis1_cod$D * dis1_cod$E +
efectos_reales_25_vec["B:D:E"] * dis1_cod$B * dis1_cod$D * dis1_cod$E +
efectos_reales_25_vec["C:D:E"] * dis1_cod$C * dis1_cod$D * dis1_cod$E +
efectos_reales_25_vec["A:B:C:D"] * dis1_cod$A * dis1_cod$B * dis1_cod$C * dis1_cod$D +
efectos_reales_25_vec["A:B:C:E"] * dis1_cod$A * dis1_cod$B * dis1_cod$C * dis1_cod$E +
efectos_reales_25_vec["A:B:D:E"] * dis1_cod$A * dis1_cod$B * dis1_cod$D * dis1_cod$E +
efectos_reales_25_vec["A:C:D:E"] * dis1_cod$A * dis1_cod$C * dis1_cod$D * dis1_cod$E +
efectos_reales_25_vec["B:C:D:E"] * dis1_cod$B * dis1_cod$C * dis1_cod$D * dis1_cod$E +
efectos_reales_25_vec["A:B:C:D:E"] * dis1_cod$A * dis1_cod$B * dis1_cod$C * dis1_cod$D * dis1_cod$E +
error
## Asignación de la respuesta al dis1_cod
dis1_cod <- cbind(dis1_cod, yrta)
## Diseño con réplicas y sin puntos centrales
dis2_cod <- dis1_cod[-c(65:69),]
## Diseño sin réplica y con cinco puntos centrales
rep1 <- c(1:32)
rep2 <- c(33:64)
seleccion_name <- sample(c("rep1","rep2"),1) #repetición a eliminar
sel <- get(seleccion_name)
dis3_cod <- dis1_cod[-sel,]
## Diseño sin réplica y con dos puntos centrales
rep1 <- c(1:32)
rep2 <- c(33:64)
seleccion_name <- sample(c("rep1","rep2"),1) #repetición a eliminar
sel <- get(seleccion_name)
rep_pc <- sample(c(65:69),3) #punto central a eliminar
dis4_cod <- dis1_cod[-c(sel,rep_pc),]
## Diseño sin réplicas y sin puntos centrales
rep1 <- c(1:32, 65:69)
rep2 <- c(33:64, 65:69)
seleccion_name <- sample(c("rep1","rep2"),1) #repetición a eliminar
sel <- get(seleccion_name)
dis6_cod <- dis1_cod[-sel,]
mod6 <- lm(yrta~A*B*C*D*E, data=dis6_cod)
graf <- suppressMessages(halfnormal(mod6, alpha = 0.05, plot=FALSE, method="Lenth"))
signif <- graf$signif
TAB6_25[i, todos_efectos_25 %in% signif] <- 1
# Modelo
## Evaluación del diseño con réplicas y con cinco puntos centrales
mod1 <- lm(yrta~A*B*C*D*E, data=dis1_cod)
## Evaluación del diseño con réplicas y sin puntos centrales
mod2 <- lm(yrta~A*B*C*D*E, data=dis2_cod)
## Evaluación del diseño sin réplicas y con cinco puntos centrales
mod3 <- lm(yrta~A*B*C*D*E, data=dis3_cod)
## Evaluación del diseño sin réplicas y con dos puntos centrales
mod4 <- lm(yrta~A*B*C*D*E, data=dis4_cod)
## Almacenar los ECM
ECM_tab_25$dis1_25[i] <- (deviance(mod1) / df.residual(mod1))
ECM_tab_25$dis2_25[i] <- (deviance(mod2) / df.residual(mod2))
ECM_tab_25$dis3_25[i] <- (deviance(mod3) / df.residual(mod3))
ECM_tab_25$dis4_25[i] <- (deviance(mod4) / df.residual(mod4))
# Lista de modelos y de tablas
mods <- list(mod1, mod2, mod3, mod4)
tabs <- list(TAB1_25, TAB2_25, TAB3_25, TAB4_25)
for (j in seq_along(mods)) {
tabs[[j]][i, ] <- sapply(1:31, function(k) {
as.integer(anova(mods[[j]])[k, 5] <= 0.05) })}
## Diseño con réplicas y con cinco puntos centrales
TAB1_25 <- tabs[[1]]
## Evaluación del diseño con réplicas y sin puntos centrales
TAB2_25 <- tabs[[2]]
## Evaluación del diseño sin réplicas y con cinco puntos centrales
TAB3_25 <- tabs[[3]]
## Evaluación del diseño sin réplicas y con dos puntos centrales
TAB4_25 <- tabs[[4]]} 4.4.2 Potencia y error tipo I
Código
## Evaluación del diseño con réplicas y con cinco puntos centrales
comp1_25 <- round(colSums(efectos_reales_25 == TAB1_25) / n * 100, 2)
pot1_25 <- round(colSums((efectos_reales_25 == 1) & (TAB1_25 == 1)) /
colSums(efectos_reales_25 == 1) * 100, 2)
err1_25 <- round(colSums((efectos_reales_25 == 0) & (TAB1_25 == 1)) /
colSums(efectos_reales_25 == 0) * 100, 2)
## Evaluación del diseño con réplicas y sin puntos centrales
comp2_25 <- round(colSums(efectos_reales_25 == TAB2_25) / n * 100, 2)
pot2_25 <- round(colSums((efectos_reales_25 == 1) & (TAB2_25 == 1)) /
colSums(efectos_reales_25 == 1) * 100, 2)
err2_25 <- round(colSums((efectos_reales_25 == 0) & (TAB2_25 == 1)) /
colSums(efectos_reales_25 == 0) * 100, 2)
## Evaluación del diseño sin réplicas y con cinco puntos centrales
comp3_25 <- round(colSums(efectos_reales_25 == TAB3_25) / n * 100, 2)
pot3_25 <- round(colSums((efectos_reales_25 == 1) & (TAB3_25 == 1)) /
colSums(efectos_reales_25 == 1) * 100, 2)
err3_25 <- round(colSums((efectos_reales_25 == 0) & (TAB3_25 == 1)) /
colSums(efectos_reales_25 == 0) * 100, 2)
## Evaluación del diseño sin réplicas y con dos puntos centrales
comp4_25 <- round(colSums(efectos_reales_25 == TAB4_25) / n * 100, 2)
pot4_25 <- round(colSums((efectos_reales_25 == 1) & (TAB4_25 == 1)) /
colSums(efectos_reales_25 == 1) * 100, 2)
err4_25 <- round(colSums((efectos_reales_25 == 0) & (TAB4_25 == 1)) /
colSums(efectos_reales_25 == 0) * 100, 2)
## Evaluación del diseño sin réplicas y sin puntos centrales
comp6_25 <- round(colSums(efectos_reales_25 == TAB6_25) / n * 100, 2)
pot6_25 <- round(colSums((efectos_reales_25 == 1) & (TAB6_25 == 1)) /
colSums(efectos_reales_25 == 1) * 100, 2)
err6_25 <- round(colSums((efectos_reales_25 == 0) & (TAB6_25 == 1)) /
colSums(efectos_reales_25 == 0) * 100, 2)4.5 Evaluación del Error Cuadrático Medio (ECM) por medidas repetidas
Para la evaluación del Error Cuadrático Medio (ECM) se diseñó la siguiente función:
Código
# X: Matriz que incluye los datos para comparar que debe estar organizada así
# C: Matriz de contrastes
# alpha: Nivel de significancia
Hotelling <- function(X, C, alpha) {
## Cálculo de la $T^2$ Hotelling
mu <- colMeans(X)
n <- nrow(X) # Número de individuos (filas de X)
p <- ncol(X) # Número de tratamientos (columnas de X)
# Matriz identidad e I - (1/n)11'
In <- diag(n)
uno <- matrix(1, n, n) # 1 x t(1)
H <- In - (1/n) * uno
# Calculo de S
S <- (1/(n-1)) * t(X) %*% H %*% X
# Cálculo de T2
T2 <- n*(t(C%*%mu))%*%(solve(C%*%S%*%t(C)))%*%(C%*%mu)
# F calculado
Fcal <- (n - p + 1) / ((n - 1)*(p - 1)) * T2
# F tabulado (crítico)
gl1 <- p-1
gl2 <- n-p+1
# Valor crítico F(0.05; p-1, n-p+1)
F_critico <- qf(1-alpha, df1 = gl1, df2 = gl2)
return(list(
T2 = as.numeric(T2),
Fcal = as.numeric(Fcal),
F_critico = F_critico))
}5 Resultados
5.1 Diseño \(2^2\)
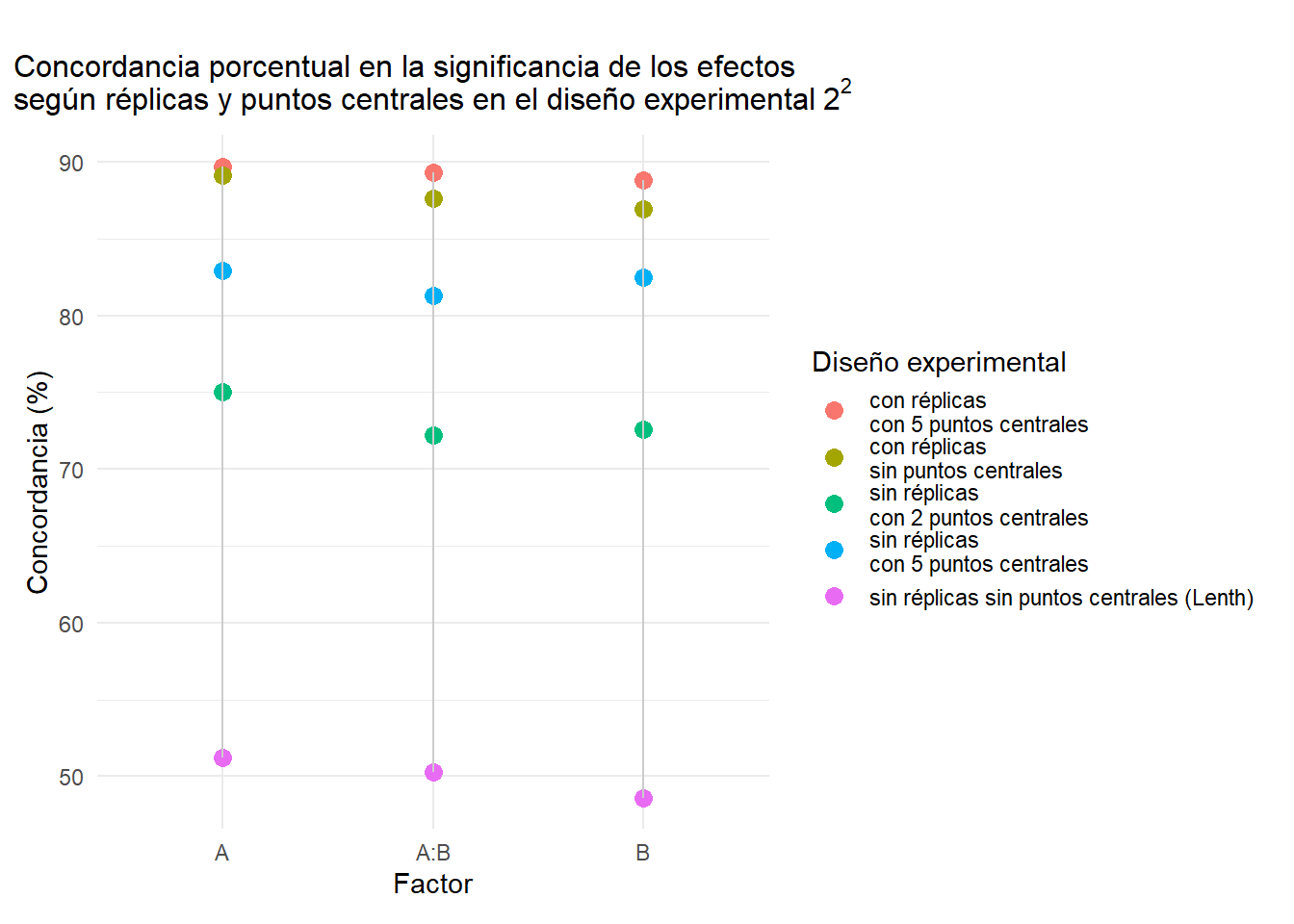
Factores | Con réplicas con 5 puntos centrales | Con réplicas sin puntos centrales | Sin réplicas con 5 puntos centrales | Sin réplicas con 2 puntos centrales | Sin réplicas sin puntos centrales (Lenth) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
Concordancia (%) | Potencia (%) | Error Tipo_I | Concordancia (%) | Potencia (%) | Error Tipo_I | Concordancia (%) | Potencia (%) | Error Tipo_I | Concordancia (%) | Potencia (%) | Error Tipo_I | Concordancia (%) | Potencia (%) | Error Tipo_I | |
A | 89.7 | 83.03 | 3.76 | 89.1 | 80.81 | 2.77 | 82.9 | 70.71 | 5.15 | 75.0 | 53.94 | 4.36 | 51.2 | 1.62 | 0.20 |
B | 88.8 | 82.88 | 4.79 | 86.9 | 79.62 | 5.21 | 82.5 | 70.00 | 3.96 | 72.6 | 51.92 | 5.00 | 48.6 | 1.73 | 0.62 |
A:B | 89.3 | 82.97 | 4.39 | 87.6 | 80.16 | 4.99 | 81.3 | 68.74 | 6.19 | 72.2 | 48.50 | 4.19 | 50.3 | 0.60 | 0.20 |
5.2 Diseño \(2^3\)
Factores | Con réplicas con 5 puntos centrales | Con réplicas sin puntos centrales | Sin réplicas con 5 puntos centrales | Sin réplicas con 2 puntos centrales | Sin réplicas sin puntos centrales (Lenth) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
Concordancia (%) | Potencia (%) | Error Tipo_I | Concordancia (%) | Potencia (%) | Error Tipo_I | Concordancia (%) | Potencia (%) | Error Tipo_I | Concordancia (%) | Potencia (%) | Error Tipo_I | Concordancia (%) | Potencia (%) | Error Tipo_I | |
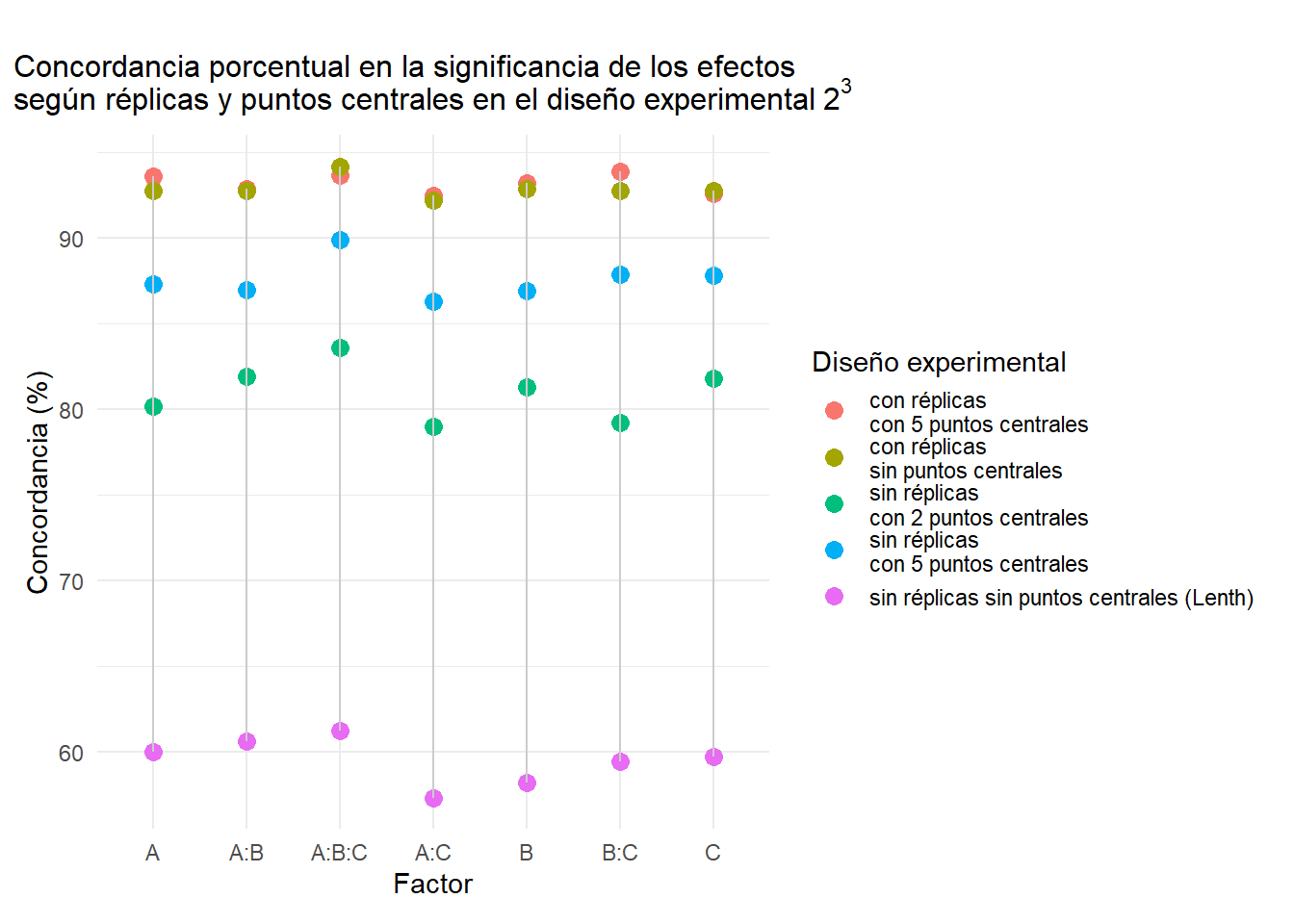
A | 93.6 | 91.70 | 4.72 | 92.8 | 90.00 | 4.72 | 87.3 | 79.15 | 5.47 | 80.2 | 63.62 | 5.09 | 60.0 | 17.45 | 2.26 |
B | 93.2 | 90.87 | 4.33 | 92.9 | 90.29 | 4.33 | 86.9 | 80.97 | 6.80 | 81.3 | 68.54 | 5.15 | 58.2 | 21.36 | 2.68 |
C | 92.6 | 90.42 | 5.21 | 92.8 | 90.22 | 4.61 | 87.8 | 82.04 | 6.41 | 81.8 | 69.06 | 5.41 | 59.7 | 22.55 | 3.01 |
A:B | 92.9 | 90.49 | 4.74 | 92.8 | 89.68 | 4.15 | 87.0 | 79.55 | 5.73 | 81.9 | 69.43 | 5.93 | 60.6 | 23.08 | 2.77 |
A:C | 92.5 | 90.27 | 5.04 | 92.2 | 89.50 | 4.83 | 86.3 | 79.39 | 6.09 | 79.0 | 64.31 | 4.83 | 57.3 | 21.37 | 3.15 |
B:C | 93.9 | 91.15 | 3.50 | 92.8 | 89.51 | 4.09 | 87.9 | 80.04 | 4.67 | 79.2 | 64.40 | 6.81 | 59.4 | 19.75 | 3.11 |
A:B:C | 93.7 | 92.99 | 5.59 | 94.2 | 92.79 | 4.39 | 89.9 | 85.17 | 5.39 | 83.6 | 72.14 | 4.99 | 61.2 | 25.85 | 3.59 |
5.3 Diseño \(2^4\)
Factores | Con réplicas con 5 puntos centrales | Con réplicas sin puntos centrales | Sin réplicas con 5 puntos centrales | Sin réplicas con 2 puntos centrales | Sin réplicas sin puntos centrales (Lenth) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
Concordancia (%) | Potencia (%) | Error Tipo_I | Concordancia (%) | Potencia (%) | Error Tipo_I | Concordancia (%) | Potencia (%) | Error Tipo_I | Concordancia (%) | Potencia (%) | Error Tipo_I | Concordancia (%) | Potencia (%) | Error Tipo_I | |
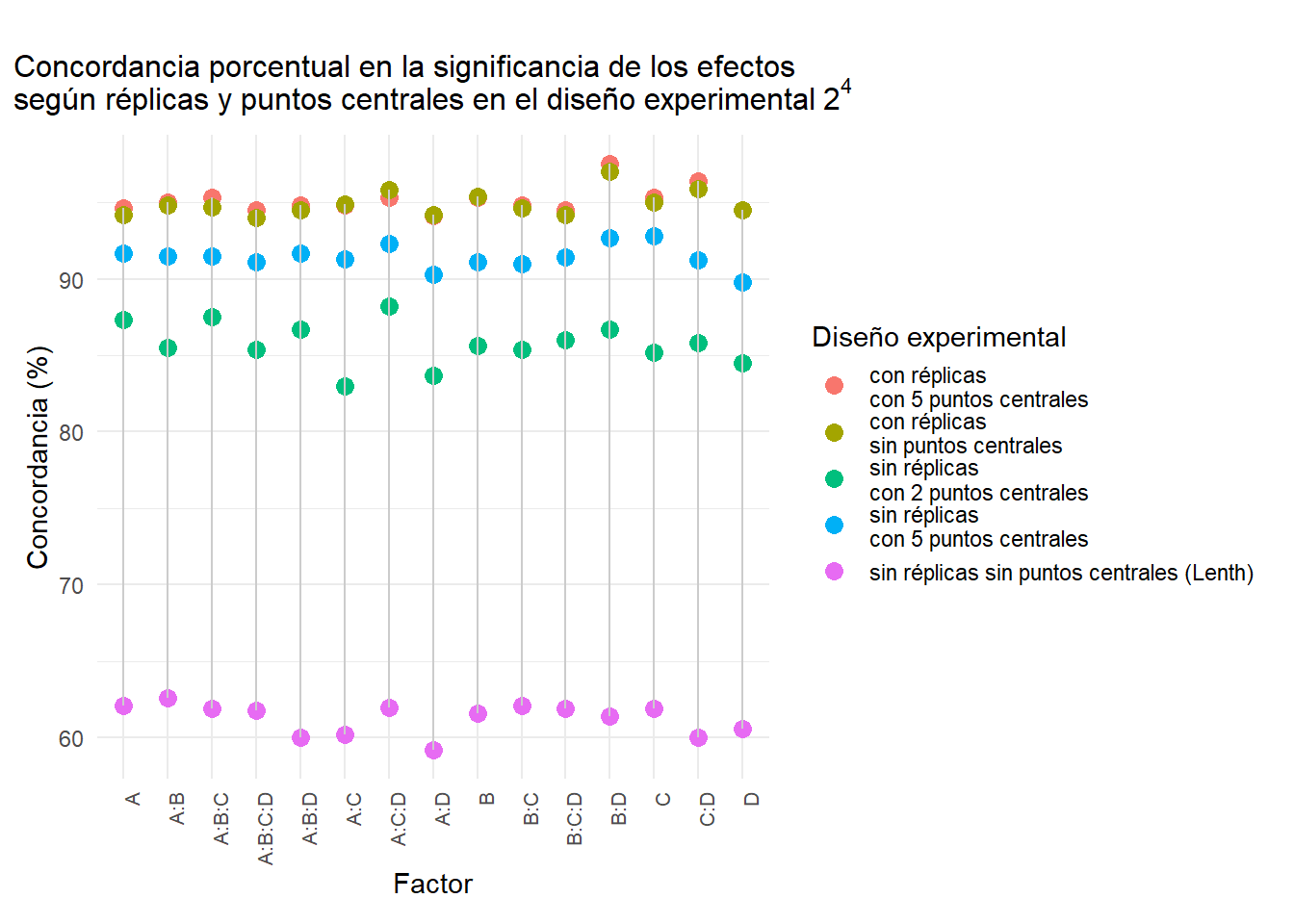
A | 94.6 | 94.13 | 4.94 | 94.2 | 93.93 | 5.53 | 91.7 | 87.45 | 4.15 | 87.3 | 79.76 | 5.34 | 62.1 | 25.51 | 2.17 |
B | 95.3 | 95.47 | 4.88 | 95.4 | 95.87 | 5.08 | 91.1 | 87.60 | 5.28 | 85.6 | 76.97 | 5.49 | 61.6 | 27.17 | 2.85 |
C | 95.3 | 96.52 | 5.87 | 95.0 | 96.32 | 6.26 | 92.8 | 88.55 | 3.13 | 85.2 | 76.48 | 6.46 | 61.9 | 25.15 | 2.94 |
D | 94.5 | 94.49 | 5.49 | 94.5 | 94.69 | 5.69 | 89.8 | 84.84 | 5.08 | 84.5 | 73.23 | 3.86 | 60.6 | 24.41 | 2.03 |
A:B | 95.0 | 94.96 | 4.96 | 94.8 | 94.56 | 4.96 | 91.5 | 88.10 | 5.16 | 85.5 | 75.00 | 4.17 | 62.6 | 27.02 | 2.38 |
A:C | 94.8 | 94.81 | 5.21 | 94.9 | 95.00 | 5.21 | 91.3 | 86.73 | 3.75 | 83.0 | 72.88 | 6.04 | 60.2 | 26.15 | 2.92 |
B:C | 94.8 | 93.54 | 3.96 | 94.6 | 93.13 | 3.96 | 91.0 | 85.45 | 3.56 | 85.4 | 75.96 | 5.35 | 62.1 | 25.66 | 2.18 |
A:D | 94.1 | 92.87 | 4.57 | 94.2 | 92.49 | 3.95 | 90.3 | 84.59 | 3.53 | 83.7 | 73.60 | 5.41 | 59.2 | 24.66 | 3.53 |
B:D | 97.5 | 97.05 | 2.03 | 97.0 | 97.05 | 3.05 | 92.7 | 90.16 | 4.67 | 86.7 | 78.15 | 4.47 | 61.4 | 26.18 | 2.24 |
C:D | 96.4 | 96.61 | 3.84 | 95.9 | 95.86 | 4.05 | 91.2 | 87.57 | 4.69 | 85.8 | 77.97 | 5.33 | 60.0 | 27.31 | 2.99 |
A:B:C | 95.3 | 96.86 | 6.31 | 94.7 | 96.46 | 7.13 | 91.5 | 88.41 | 5.30 | 87.5 | 80.35 | 5.09 | 61.9 | 29.27 | 4.28 |
A:B:D | 94.8 | 94.98 | 5.38 | 94.5 | 94.78 | 5.78 | 91.7 | 88.15 | 4.78 | 86.7 | 78.31 | 4.98 | 60.0 | 22.89 | 3.19 |
A:C:D | 95.3 | 95.83 | 5.24 | 95.8 | 95.83 | 4.23 | 92.3 | 88.89 | 4.23 | 88.2 | 81.35 | 4.84 | 62.0 | 27.58 | 3.02 |
B:C:D | 94.5 | 94.64 | 5.65 | 94.2 | 94.64 | 6.25 | 91.4 | 88.29 | 5.44 | 86.0 | 77.98 | 5.85 | 61.9 | 27.38 | 3.02 |
A:B:C:D | 94.5 | 95.30 | 6.34 | 94.0 | 94.91 | 6.95 | 91.1 | 86.69 | 4.29 | 85.4 | 75.93 | 4.70 | 61.8 | 27.59 | 2.45 |
5.4 Diseño \(2^5\)
Factores | Con réplicas con 5 puntos centrales | Con réplicas sin puntos centrales | Sin réplicas con 5 puntos centrales | Sin réplicas con 2 puntos centrales | Sin réplicas sin puntos centrales (Lenth) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
Concordancia (%) | Potencia (%) | Error Tipo_I | Concordancia (%) | Potencia (%) | Error Tipo_I | Concordancia (%) | Potencia (%) | Error Tipo_I | Concordancia (%) | Potencia (%) | Error Tipo_I | Concordancia (%) | Potencia (%) | Error Tipo_I | |
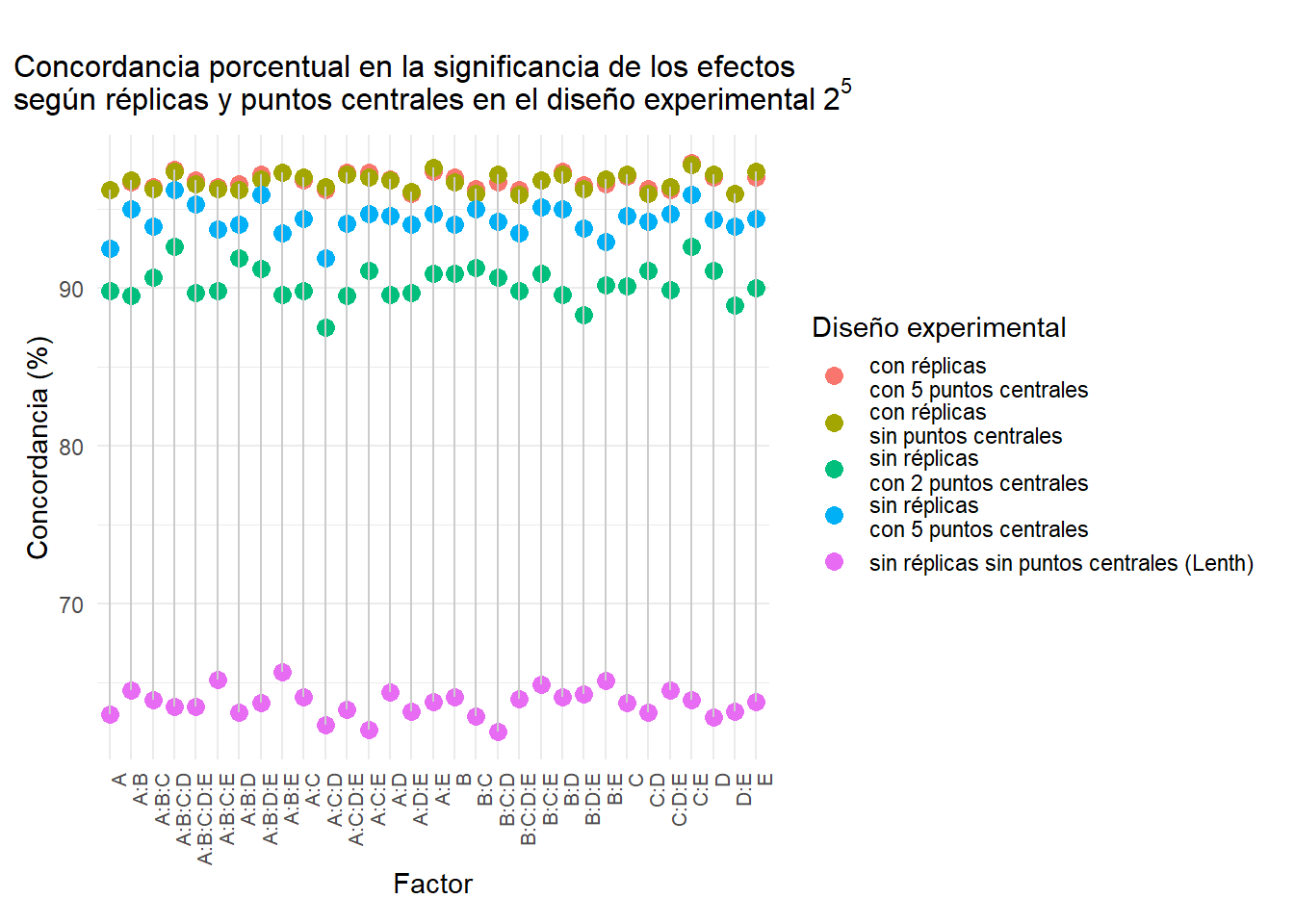
A | 96.2 | 97.24 | 4.87 | 96.2 | 97.04 | 4.67 | 92.5 | 90.93 | 5.88 | 89.8 | 84.81 | 5.07 | 63.0 | 30.18 | 3.25 |
B | 97.0 | 99.20 | 5.17 | 96.7 | 98.79 | 5.37 | 94.0 | 93.36 | 5.37 | 90.9 | 87.93 | 6.16 | 64.1 | 31.39 | 3.58 |
C | 97.1 | 98.58 | 4.35 | 97.2 | 98.58 | 4.15 | 94.6 | 93.72 | 4.55 | 90.1 | 87.04 | 6.92 | 63.7 | 30.16 | 3.56 |
D | 97.0 | 98.84 | 4.96 | 97.2 | 98.84 | 4.55 | 94.3 | 93.80 | 5.17 | 91.1 | 87.79 | 5.37 | 62.8 | 31.01 | 3.31 |
E | 97.0 | 98.62 | 4.67 | 97.4 | 98.62 | 3.85 | 94.4 | 93.89 | 5.07 | 90.0 | 85.40 | 5.27 | 63.8 | 31.36 | 2.84 |
A:B | 96.7 | 97.64 | 4.28 | 96.8 | 97.84 | 4.28 | 95.0 | 93.71 | 3.67 | 89.5 | 85.46 | 6.31 | 64.5 | 32.42 | 2.24 |
A:C | 96.8 | 97.97 | 4.58 | 97.0 | 98.52 | 4.79 | 94.4 | 94.09 | 5.23 | 89.8 | 86.88 | 6.75 | 64.1 | 35.49 | 2.18 |
B:C | 96.3 | 98.28 | 5.87 | 96.0 | 97.90 | 6.08 | 95.0 | 94.07 | 3.98 | 91.3 | 87.95 | 5.03 | 62.9 | 32.70 | 3.98 |
A:D | 96.9 | 98.00 | 4.20 | 96.8 | 98.20 | 4.60 | 94.6 | 93.80 | 4.60 | 89.6 | 86.20 | 7.00 | 64.4 | 31.60 | 2.80 |
B:D | 97.4 | 99.24 | 4.66 | 97.2 | 99.43 | 5.30 | 95.0 | 94.70 | 4.66 | 89.6 | 86.55 | 6.99 | 64.1 | 34.85 | 3.18 |
C:D | 96.3 | 98.84 | 6.40 | 96.0 | 98.64 | 6.82 | 94.2 | 93.41 | 4.96 | 91.1 | 88.76 | 6.40 | 63.1 | 32.56 | 4.34 |
A:E | 97.4 | 98.97 | 4.09 | 97.6 | 98.97 | 3.70 | 94.7 | 94.03 | 4.67 | 90.9 | 86.83 | 5.25 | 63.8 | 28.19 | 2.53 |
B:E | 96.6 | 97.87 | 4.76 | 96.9 | 97.87 | 4.14 | 92.9 | 91.88 | 6.00 | 90.2 | 85.11 | 4.35 | 65.1 | 35.01 | 2.69 |
C:E | 97.9 | 99.40 | 3.61 | 97.8 | 99.20 | 3.61 | 95.9 | 94.81 | 3.01 | 92.6 | 89.42 | 4.21 | 63.9 | 29.74 | 1.80 |
D:E | 96.0 | 98.25 | 6.37 | 96.0 | 98.05 | 6.16 | 93.9 | 92.98 | 5.13 | 88.9 | 84.99 | 6.98 | 63.2 | 30.60 | 2.46 |
A:B:C | 96.4 | 98.02 | 5.24 | 96.3 | 98.02 | 5.44 | 93.9 | 93.45 | 5.65 | 90.7 | 86.11 | 4.64 | 63.9 | 30.36 | 2.02 |
A:B:D | 96.6 | 98.01 | 4.82 | 96.2 | 97.61 | 5.22 | 94.0 | 92.83 | 4.82 | 91.9 | 87.85 | 4.02 | 63.1 | 30.28 | 3.82 |
A:C:D | 96.2 | 96.66 | 4.34 | 96.4 | 96.85 | 4.12 | 91.9 | 90.72 | 6.72 | 87.5 | 82.37 | 6.51 | 62.3 | 32.65 | 3.04 |
B:C:D | 96.7 | 97.89 | 4.60 | 97.2 | 98.28 | 3.97 | 94.2 | 93.30 | 4.81 | 90.7 | 86.02 | 4.18 | 61.9 | 30.08 | 3.35 |
A:B:E | 97.3 | 98.39 | 3.78 | 97.3 | 98.39 | 3.78 | 93.5 | 92.76 | 5.77 | 89.6 | 84.31 | 5.17 | 65.7 | 33.80 | 2.78 |
A:C:E | 97.3 | 98.43 | 3.87 | 97.0 | 98.43 | 4.48 | 94.7 | 94.50 | 5.09 | 91.1 | 88.21 | 5.91 | 62.0 | 27.50 | 2.24 |
B:C:E | 96.8 | 98.25 | 4.74 | 96.8 | 98.25 | 4.74 | 95.1 | 94.76 | 4.54 | 90.9 | 87.96 | 5.98 | 64.9 | 33.98 | 2.27 |
A:D:E | 96.0 | 98.04 | 6.12 | 96.1 | 97.84 | 5.71 | 94.0 | 92.55 | 4.49 | 89.7 | 84.90 | 5.31 | 63.2 | 30.39 | 2.65 |
B:D:E | 96.5 | 98.59 | 5.57 | 96.3 | 98.59 | 5.96 | 93.8 | 91.75 | 4.17 | 88.3 | 83.50 | 6.96 | 64.3 | 30.99 | 2.78 |
C:D:E | 96.2 | 97.78 | 5.36 | 96.4 | 97.78 | 4.96 | 94.7 | 92.94 | 3.57 | 89.9 | 84.68 | 4.96 | 64.5 | 31.25 | 2.78 |
A:B:C:D | 97.5 | 99.42 | 4.55 | 97.4 | 99.42 | 4.75 | 96.2 | 95.54 | 3.10 | 92.6 | 89.15 | 3.72 | 63.5 | 31.01 | 1.86 |
A:B:C:E | 96.4 | 97.60 | 4.79 | 96.3 | 97.60 | 4.99 | 93.7 | 92.18 | 4.79 | 89.8 | 84.57 | 4.99 | 65.2 | 33.07 | 2.79 |
A:B:D:E | 97.2 | 99.22 | 4.91 | 96.9 | 99.02 | 5.32 | 95.9 | 96.28 | 4.50 | 91.2 | 87.67 | 5.11 | 63.7 | 32.29 | 3.48 |
A:C:D:E | 97.3 | 98.50 | 4.07 | 97.2 | 98.50 | 4.28 | 94.1 | 92.87 | 4.50 | 89.5 | 85.55 | 6.00 | 63.3 | 33.77 | 3.00 |
B:C:D:E | 96.2 | 97.44 | 5.07 | 95.9 | 97.24 | 5.48 | 93.5 | 91.91 | 4.87 | 89.8 | 84.62 | 4.87 | 64.0 | 32.94 | 4.06 |
A:B:C:D:E | 96.8 | 98.64 | 5.15 | 96.6 | 98.64 | 5.57 | 95.3 | 93.79 | 3.09 | 89.7 | 85.05 | 5.36 | 63.5 | 31.65 | 2.68 |
5.5 Evaluación del ECM
5.5.1 Análisis descriptivo de los ECM por diseño
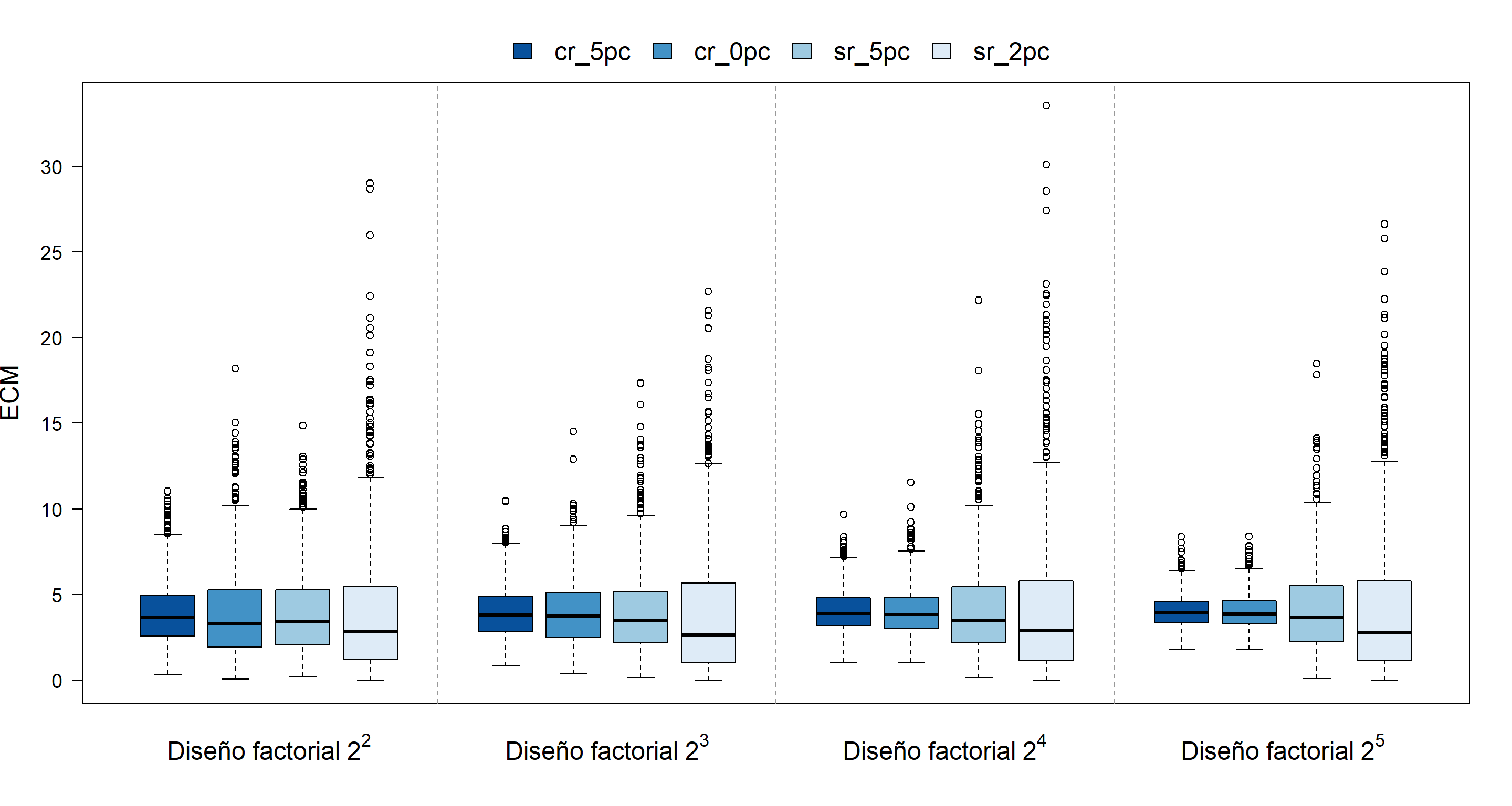
5.5.2 Matriz de contrastes generales \(C_1\)
Diseño | T² | F_calculado | F_crítico | Decisión |
|---|---|---|---|---|
Diseño factorial 2² | 0.27 | 0.09 | 2.61 | No se rechaza H₀ |
Diseño factorial 2³ | 2.67 | 0.89 | 2.61 | No se rechaza H₀ |
Diseño factorial 2⁴ | 2.21 | 0.74 | 2.61 | No se rechaza H₀ |
Diseño factorial 2⁵ | 4.96 | 1.65 | 2.61 | No se rechaza H₀ |