4  Replicación en R de caso de estudio: Charoo et al. (2012)

Quality by design approach for formulation development: a case study of dispersible tablets, artículo escrito por Charoo et al. (2012)

5 Artículo de estudio

En el artículo publicado por Charoo et al. (2012), “Quality by design approach for formulation development: a case study of dispersible tablets”, se describen varios diseños experimentales relacionados con la fabricación de tabletas orodispersables de diclofenaco. A continuación, se muestra una réplica del Estudio No. 7 descrito en el artículo de referencia, orientado a evaluar la influencia de la proporción de desintegrante (DES) y el tiempo de mezcla (TIEMPO) sobre el tiempo de desintegración (TD).

Nota

Véase “Guía para la implementación de diseños experimentales en la industria farmacéutica” para una explicación detallada de los cálculos presentados.

Librerías requeridas: dplyr, flextable, car, nortest

6 Simulación de respuestas

El artículo de Charoo et al. (2012) reporta únicamente el valor promedio de las tres réplicas junto con su desviación estándar, por lo que se requiere simular los datos individuales. Para este propósito, se construyó la función simuesblo, disponible en el archivo funciones.R del repositorio ncortes/Disexp_Industria_Farmaceutica en GitHub (funcionesR?).

Código 
desintegration_mean <- c(42, 56, 55, 70)     # Datos tomados del artículo - estudio 7 
desintegration_sd <- c(rep(1.5, 4))          # Datos de desviación estándar sugeridos
TD <- as.vector(simuesblo(desintegration_mean, desintegration_sd, 2, 2))

Los valores simulados para el tiempo de desintegración son: 41.16, 58.34, 55.19, 70.69, 41.65, 56.11, 57.57, 68.1

7 Construcción del diseño experimental

Código 
# Construcción del diseño (notación codificada)
dis <- data.frame(
  TRAT = c("T1", "T2", "T3", "T4", "T1", "T2", "T3", "T4"),
  REP = c(rep("R1", 4), rep("R2", 4)),
  TIEMPO = rep(c(-1, -1, 1, 1),2),
  DES =   rep(c(-1, 1, -1, 1),2),
  TD)

TRAT

REP

TIEMPO

DES

TD

T1

R1

-1

-1

41.16

T2

R1

-1

1

58.34

T3

R1

1

-1

55.19

T4

R1

1

1

70.69

T1

R2

-1

-1

41.65

T2

R2

-1

1

56.11

T3

R2

1

-1

57.57

T4

R2

1

1

68.10

Tabla 7.1: Construcción del diseño factorial completo 2²

8 Modelo de regresión

Código 
mod <- lm(TD ~ TIEMPO*DES, data = dis)
summary(mod)

Call:
lm(formula = TD ~ TIEMPO * DES, data = dis)

Residuals:
     1      2      3      4      5      6      7      8 
-0.245  1.115 -1.190  1.295  0.245 -1.115  1.190 -1.295 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  56.1012     0.5242 107.025 4.57e-08 ***
TIEMPO        6.7863     0.5242  12.946 0.000205 ***
DES           7.2088     0.5242  13.752 0.000162 ***
TIEMPO:DES   -0.7013     0.5242  -1.338 0.251961    
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 1.483 on 4 degrees of freedom
Multiple R-squared:  0.989, Adjusted R-squared:  0.9807 
F-statistic: 119.5 on 3 and 4 DF,  p-value: 0.0002274

9 ANOVA

Código 
anova(mod)
Analysis of Variance Table

Response: TD
           Df Sum Sq Mean Sq  F value    Pr(>F)    
TIEMPO      1 368.43  368.43 167.6042 0.0002054 ***
DES         1 415.73  415.73 189.1234 0.0001620 ***
TIEMPO:DES  1   3.93    3.93   1.7897 0.2519609    
Residuals   4   8.79    2.20                       
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

10 Verificación de supuestos

Código 
# Residuos del modelo
residuales <- mod$residuals

# Prueba de homogeneidad de varianzas
bt <- bartlett.test(residuales~TRAT, data=dis)

# Prueba de normalidad de Kolmogorov-Smirnov
ks <- ks.test(residuales,"pnorm",mean(residuales), sd(residuales))

# Prueba de normalidad de Shapiro-Wilk
sp <- shapiro.test(residuales)

Pruebas

Estadístico

p-valor

Interpretación

Prueba de bartlett

1.4882

0.6850

Los residuales son homocedásticos

Kolmogorov-Smirnov

0.2151

0.7823

Los residuales son normales

Shapiro-Wilk

0.8526

0.1013

Los residuales son normales

Tabla 10.1: Análisis de supuestos de los residuales estandarizados

11 Graficos de interacción

Código 
interaction.plot(
  x.factor   = factor(dis$TIEMPO),
  trace.factor = factor(dis$DES),
  response   = as.numeric(dis$TD),
  fun        = mean,
  type       = "b",
  col        = c("blue", "black"),  
  lty        = c(1, 1),             
  lwd        = 3,                   
  pch        = c(19, 19),           
  xlab       = "TIEMPO",
  ylab       = "Tiempo de desintegración (TD)",
  trace.label = "DES")
Figura 11.1: Gráfico de interacción

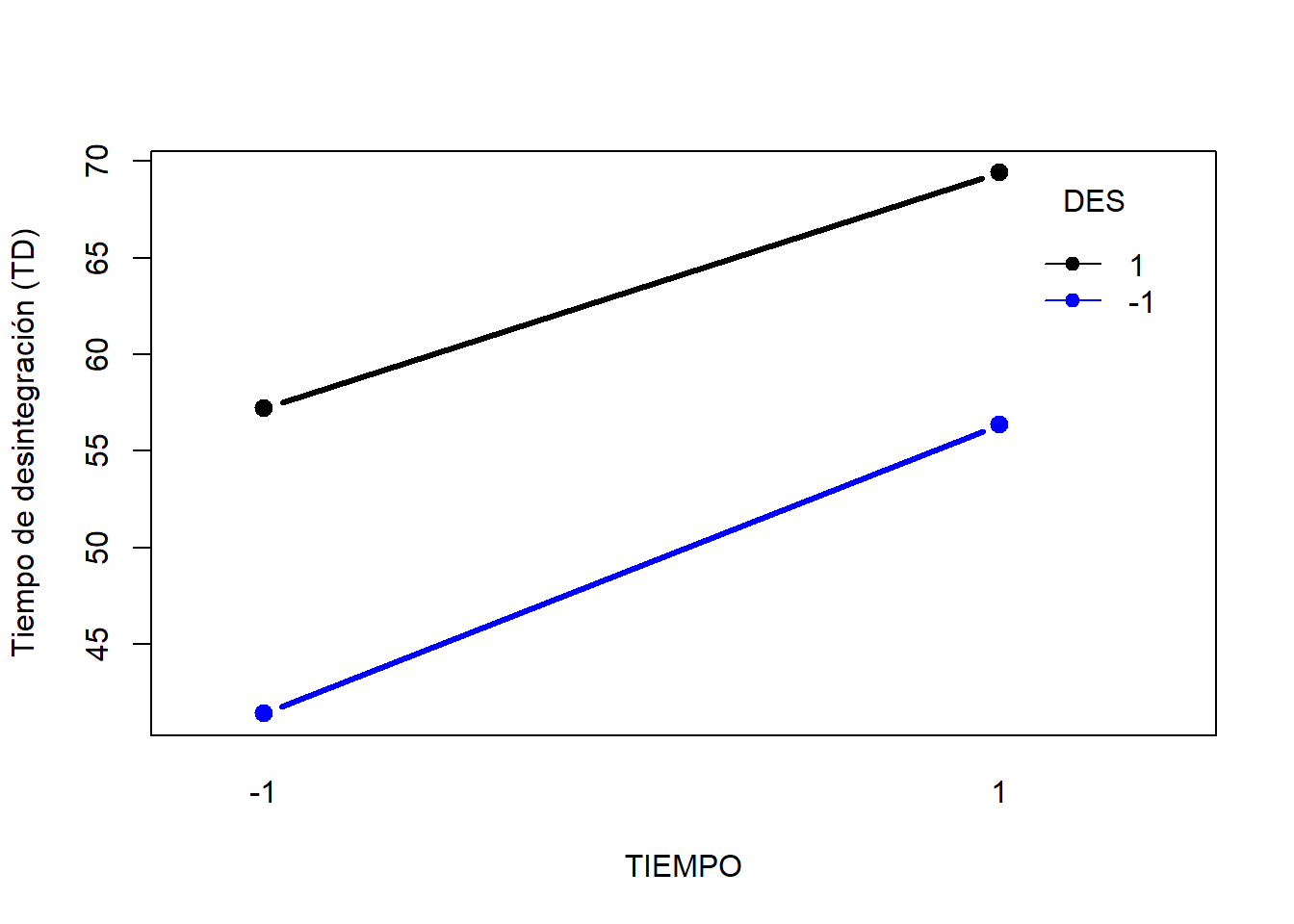
12 Gráfico de superficie

Código 
# Definir la malla
x1 <- seq(min(dis$TIEMPO), max(dis$TIEMPO), length = 30)
x2 <- seq(min(dis$DES), max(dis$DES), length = 30)

# Crear cuadrícula
grid <- expand.grid(TIEMPO = x1, DES = x2)

# Predecir con el modelo en cada punto de la malla
grid$z <- predict(mod, newdata = grid)

# Pasar a matriz para persp/contour
z <- matrix(grid$z, nrow = length(x1), ncol = length(x2))

# --- Gráfico de superficie ---
persp(x1, x2, z,
      theta = 30, phi = 25,       
      col = NA,                   
      border = "steelblue",        
      lwd = 1,                   
      ticktype = "detailed",
      xlab = "TIEMPO", ylab = "DES", zlab = "TD",
      cex.lab = 0.8,      
      cex.axis = 0.8,     
      cex.main = 0.8,     
      main = "Gráfico de superficie de respuesta")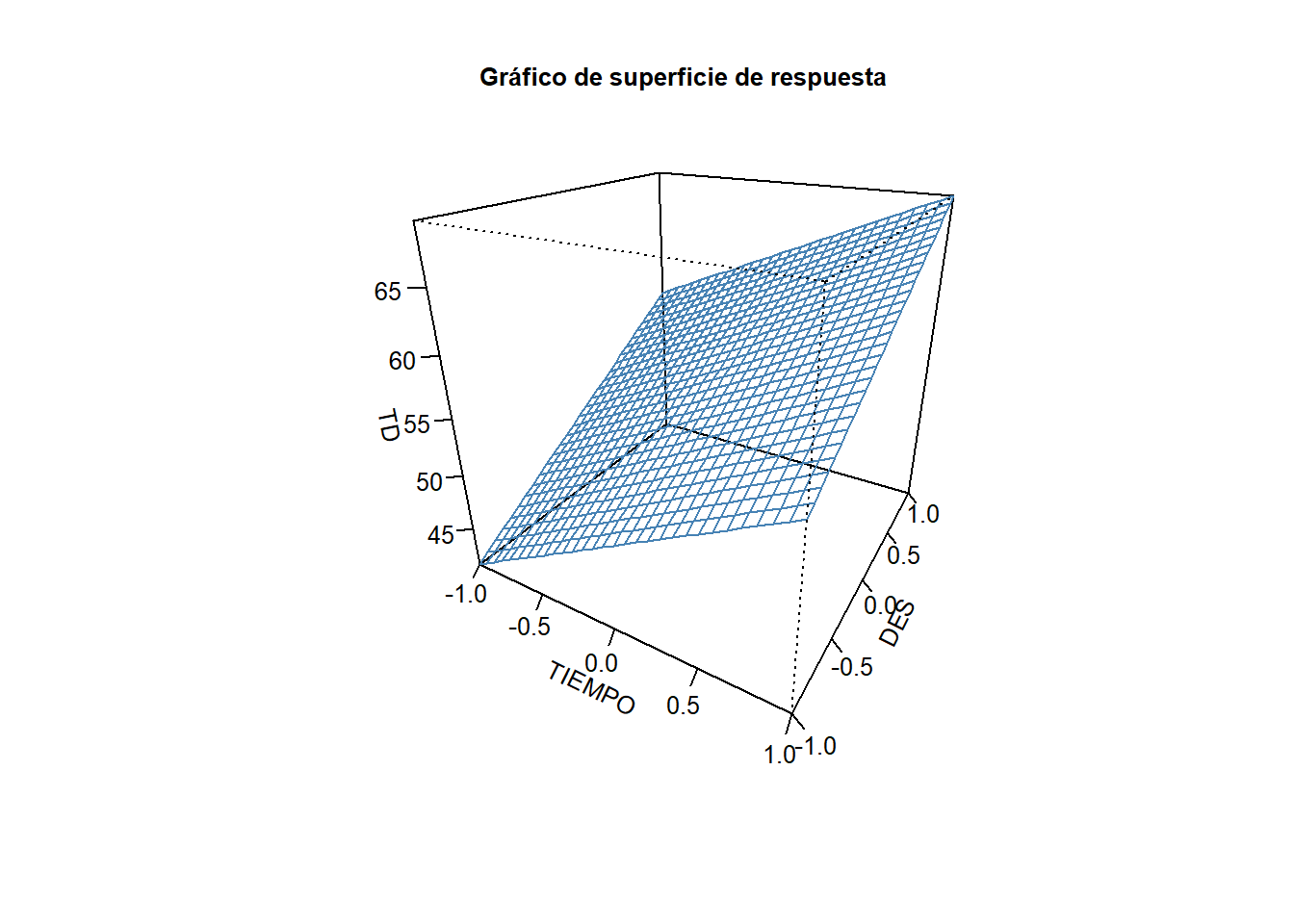
Figura 12.1: Gráfico de superficie

13 Gráfico de contorno

Código 
# --- Gráfico de contorno ---
contour(x1, x2, z,
        nlevels = 15,            
        col = "steelblue", lwd = 1.2,
        xlab = "TIEMPO", ylab = "DES",
        main = "Gráfico de contorno")
Figura 13.1: Gráfico de contorno
Charoo, Naseem A, Areeg AA Shamsher, Ahmed S Zidan, y Ziyaur Rahman. 2012. «Quality by design approach for formulation development: a case study of dispersible tablets». International journal of pharmaceutics 423 (2): 167-78.
Volver arriba