3  Comparación de métodos de imputación en diseños experimentales de mezclas

Nota

El presente documento corresponde a un apartado del trabajo titulado “Guía para la implementación de diseños experimentales en la industria farmacéutica”, presentado por Nathalia Cortés Duque como requisito para optar al título de Magíster en Ciencias - Estadística de la Universidad Nacional de Colombia.

4 Metodología

En los diseños de mezclas, se pueden presentar valores respuesta faltantes. Aunque existen diversos métodos de imputación, pocas veces se analiza de qué región del diseño experimental —ya sea de los vértices del simplex, de los puntos axiales o del centroide— proviene la ausencia de datos antes de seleccionar el procedimiento de imputación más apropiado.

La imputación constituye una herramienta estadística ampliamente utilizada para abordar este tipo de situaciones, especialmente cuando la falta de datos tiene un componente aleatorio. Siguiendo lo descrito por Wongoutong (2022) para diseños centrales compuestos, En este estudio se evaluó el efecto de un único valor de respuesta faltante en distintas zonas del diseño de mezclas (vértices, puntos axiales y centroide), aplicando diferentes métodos de imputación —media global, media parcial, regresión y K-vecinos más cercanos (KNN).

• Imputación por la media global: consiste en reemplazar el valor faltante por la media de los datos disponibles.

• Imputación por media parcial: el valor faltante se sustituye por la media de los valores no faltantes pertenecientes al mismo tipo de punto. Por ejemplo, si el dato perdido corresponde a un punto centrado en las caras, este se reemplaza por el promedio de los demás valores disponibles de tratamientos centrados en las caras.

• Imputación por K vecinos más cercanos: el valor faltante se reemplaza por el promedio de los valores correspondientes a las observaciones más cercanas. Para ello, se definió una medida de proximidad entre los tratamientos; en este caso, se utilizó la distancia euclidiana. La clasificación de los puntos se encuentra en el Anexo 1.

• Imputación por regresión: se ajusta un modelo de regresión con los datos completos y, a partir de este, se estima el valor faltante. En este trabajo se consideran los modelos de regresión propios de los diseños de mezclas, tanto en su forma lineal como cuadrática.

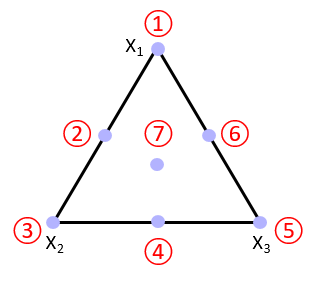
La caracterización de los tratamientos experimentales, conforme a la ubicación mostrada en la Figura 4.1, se presenta en la Tabla 12.2. El desempeño de los métodos de imputación se evaluó a partir de la generación de 1000 simulaciones de diseños de mezclas simplex-centroide, construidos bajo el modelo de regresión lineal característico de este tipo de diseños. En cada simulación se eliminó aleatoriamente un dato, lo que permitió comparar el valor imputado por cada método con el valor verdadero y, a partir de esta comparación, calcular el error. Se emplearon dos índicadores para cuantificar el error: el EAM (Error Absoluto Medio) y el RECM (Raíz del Error Cuadrático Medio), ambos calculados entre los valores reales y los imputados.

\[EAM = \frac{1}{n} \sum_{i=1}^{n} \left| y_i - \hat{y}_i \right|\]

\[RECM = \sqrt{\frac{1}{n} \sum_{i=1}^{n} \left( y_i - \hat{y}_i \right)^2}\]

donde \(y_i\) es el dato real, \(\hat{y}_i\) el dato imputado y \(n\) corresponde al número de observaciones disponibles utilizadas en el cálculo según el método de imputación.

Librerías requeridas: dplyr, flextable, mixexp

Figura 4.1: Tratamientos experimentales del diseño simplex con centroide

Tratamiento	x1	x2	x3
T1	1.00	0.00	0.00
T2	0.50	0.50	0.00
T3	0.00	1.00	0.00
T4	0.00	0.50	0.50
T5	0.00	0.00	1.00
T6	0.50	0.00	0.50
T7	0.33	0.33	0.33
T7	0.33	0.33	0.33
T7	0.33	0.33	0.33

Tabla 4.1: Diseño simplex con centroide

5 Simulación de datos

# Funcion para generar respuestas para diseños de mezclas 
## des: dataframe que indica el diseño de mezclas
## sd: Desviación deseada para la generación del error
## mod: Tipo de modelo que se desea usar la para simulación de las respuestas, donde:
## 1: Modelo lineal
## 2: Modelo cuadrático
## 3: Modelo cúbico

gen_scheffe <- function(des, 
                        sd = 1, 
                        mod = c(1,2,3)) {
  # explicar que es mod =1, 2 y 3
  
  x1 <- des$x1; x2 <- des$x2; x3 <- des$x3 # las componentes
  beta = round(runif(7, -10, 10),2)
  
  # Modelo lineal
  if (mod == 1)
  {y_mean <- beta[1]*x1 + beta[2]*x2 + beta[3]*x3} 
  
  # Modelo cuadrático
  if (mod == 2)
  {y_mean <- beta[1]*x1 + beta[2]*x2 + beta[3]*x3 +
    beta[4]*x1*x2 + beta[5]*x1*x3 + beta[6]*x2*x3}
  
  # Modelo cúbico especial
  if (mod == 3)
  {y_mean <- beta[1]*x1 + beta[2]*x2 + beta[3]*x3 +
      beta[4]*x1*x2 + beta[5]*x1*x3 + beta[6]*x2*x3 +
      beta[7]*x1*x2*x3}
  
  # Adición de error
  yrta <- y_mean + rnorm(length(y_mean), mean = 0, sd = sd)
  return(yrta)
}

5.1 Modelo lineal

ymat <- matrix(NA, nrow = nrow(des), ncol = n)

for (i in 1:n) {
    ymat[, i] <- gen_scheffe(des, 
                             sd = 1,
                             mod = 1)
  }
  colnames(ymat) <- paste0("y", 1:n)
  resultados_df <- cbind(des, as.data.frame(ymat)) 

Se simulan 1000 modelos generados a partir de un modelo lineal canónico de Scheffé. A continuación, se presenta uno de ellos:

     
   coefficients   Std.err   t.value         Prob
x1    -8.685797 0.9906899 -8.767423 0.0001219853
x2     2.367515 0.9948362  2.379803 0.0547828282
x3     6.253771 0.9948362  6.286232 0.0007542658
     
Residual standard error:  1.237552  on  6 degrees of freedom 
Corrected Multiple R-squared:  0.9423512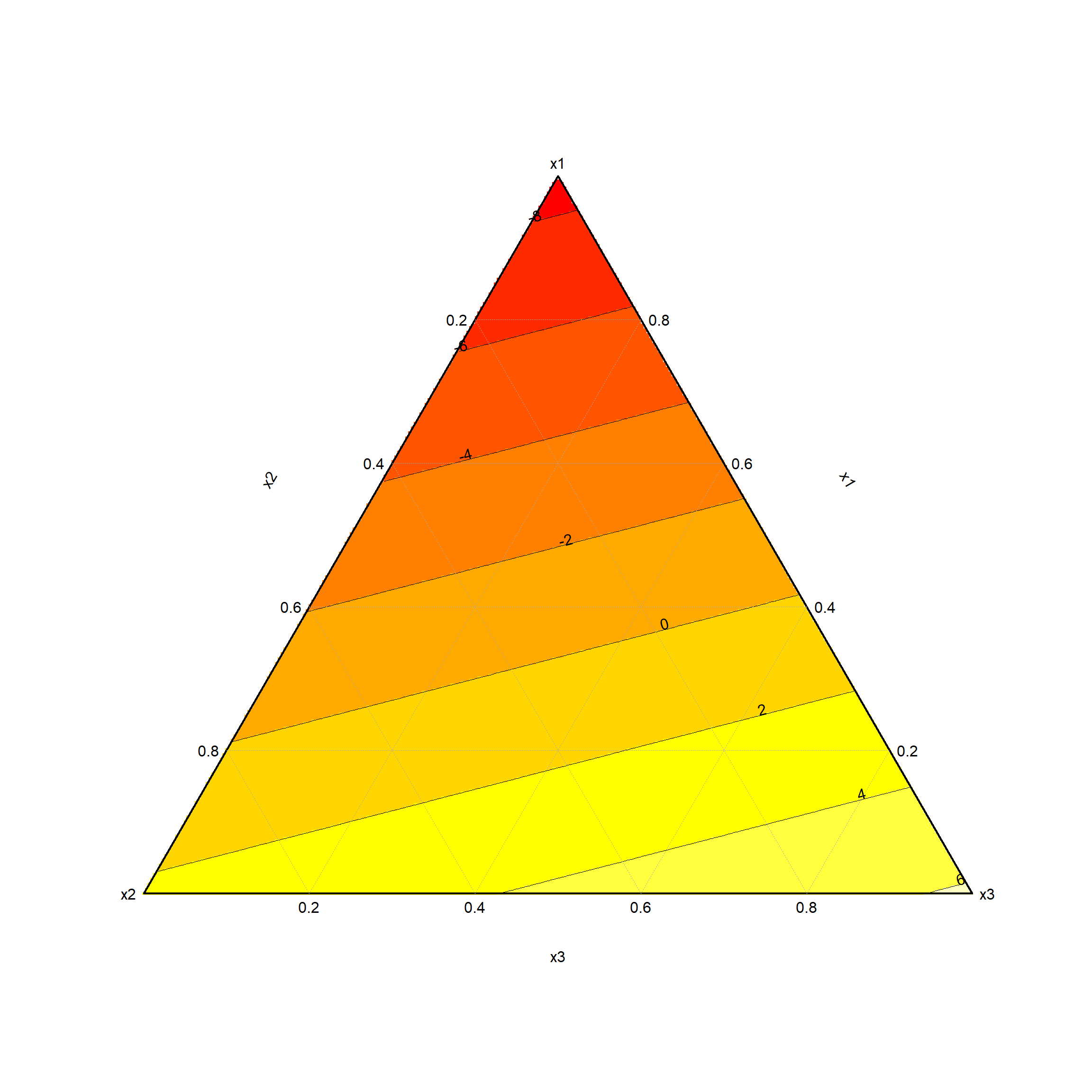

Figura 5.1: Diseño simplex con centroide simulado con modelo lineal - Gráfica de contorno

5.1.1 Método 1: Imputación por la media global

abserror11 <- matrix(NA, ncol = 6, nrow = n)
errorcua11 <- matrix(NA, ncol = 6, nrow = n)

for (i in 1:6) {
  tab2 <- resultados_df[-i, -(1:3)]
  vr <- as.numeric(resultados_df[i, -(1:3)])      # valor real (vector)
  ve <- as.numeric(apply(tab2, 2, mean))          # valor estimado (vector)
  
  abserror11[,i] <- abs(vr - ve)
  errorcua11[,i] <- (vr - ve)^2

  resumenli[1, i+2] <- round(mean(abserror11[,i]),2)
  resumenli[2, i+2] <- round(sqrt(mean(errorcua11[,i])),2)
  }
colnames(abserror11) <- paste0("T", 1:6)

5.1.2 Método 2: Imputación por media parcial

abserror21 <- matrix(NA, ncol = 6, nrow = n)
errorcua21 <- matrix(NA, ncol = 6, nrow = n)

for (i in 1:6) {
  vr <- as.numeric(resultados_df[i,-(1:3)])   # valor real
  
  simg1 <- c(1,3,5)   #Similares grupo 1
  simg2 <- c(2,4,6)   #Similares grupo 2
  
  grupo <- if (i %in% simg1) simg1 else simg2
  grupo_sin_sel <- grupo[grupo != i]
  
  # Calcular promedio por columnas para las filas de ese grupo
  ve<- colMeans(resultados_df[grupo_sin_sel, -c(1:3)])  # valor estimado
  
  abserror21[,i] <- (abs(vr - ve))         
  errorcua21[,i] <- (vr - ve)^2

  resumenli[3, i+2] <- round(mean(abserror21[,i]),2)
  resumenli[4, i+2] <- round(sqrt(mean(errorcua21[,i])),2)
  }

colnames(abserror21) <- paste0("T", 1:6)

5.1.3 Método 3: Imputación por vecinos más cercanos (KNN)

Los vecinos más cercanos corresponden a aquellos tratamientos que, en la columna de clasificación de la tabla Tabla 12.2, presentan el valor igual a 1, es decir, a los tratamintos que presentaron menor distancia euclideana entre ellos.

abserror31 <- matrix(NA, ncol = 6, nrow = n)
errorcua31 <- matrix(NA, ncol = 6, nrow = n)

for (i in 1:6) {
  vr <- as.numeric(resultados_df[i,-(1:3)])   # valor real
  
  vec <- tab_pesos %>% 
        filter(punto_inicial == i, clasificacion == 1) %>% 
        pull(punto_final)
  
  # Calcular promedio por columnas para las filas de ese grupo
  ve<- colMeans(resultados_df[vec, -c(1:3)])  # valor estimado
  
  abserror31[,i] <- (abs(vr - ve))         
  errorcua31[,i] <- (vr - ve)^2
  
  resumenli[5, i+2] <- round(mean(abserror31[,i]),2)
  resumenli[6, i+2] <- round(sqrt(mean(errorcua31[,i])),2)
  }

colnames(abserror31) <- paste0("T", 1:6)

5.1.4 Método 4A: Modelo de regresion lineal canónico de Scheffé

abserror411 <- matrix(NA, ncol = 6, nrow = n)
errorcua411 <- matrix(NA, ncol = 6, nrow = n)

for (i in 1:6) {
  vr <- as.numeric(resultados_df[i,-(1:3)])   # valor real
  ve <- numeric(n)                            # valor predicho
  des_dfp <- resultados_df[-i,]
  mod <- vector("list", n)   # lista para guardar los modelos
  
  # definición de los 7 tratamientos del simplex
  tratamientos <- list(
    c(1, 0, 0),
    c(0.5, 0.5, 0),
    c(0, 1, 0),
    c(0, 0.5, 0.5),
    c(0, 0, 1),
    c(0.5, 0, 0.5),
    c(1/3, 1/3, 1/3, 1/3, 1/3, 1/3, 1/3, 1/3, 1/3)
    )

    for (j in 1:n) {
      # construir fórmula dinámica: yi ~ -1 + x1 + x2 + x3
      f <- as.formula(paste0("y", j, " ~ -1 + x1 + x2 + x3"))  
      
      # ajustar modelo
      mod[[j]] <- lm(f, data = des_dfp)
      
      # armar newdata según tratamiento_sel
      newdata <- data.frame(matrix(tratamientos[[i]], nrow = 1))
      colnames(newdata) <- c("x1","x2","x3")
      
      # predecir
      ve[j] <- round(predict(mod[[j]], newdata = newdata),2)
      }

  abserror411[,i] <- (abs(vr - ve))         
  errorcua411[,i] <- (vr - ve)^2
  
  resumenli[7, i+2] <- round(mean(abserror411[,i]),2)
  resumenli[8, i+2] <- round(sqrt(mean(errorcua411[,i])),2)
  }

colnames(abserror411) <- paste0("T", 1:6)

5.1.5 Método 4B: Modelo de regresion cuadrático canónico de Scheffé

abserror421 <- matrix(NA, ncol = 6, nrow = n)
errorcua421 <- matrix(NA, ncol = 6, nrow = n)

mod <- vector("list", n)
coefs    <- matrix(NA, nrow = n, ncol = 6)
colnames(coefs) <- c("x1c","x2c","x3c",
                     "x1c_x2c", "x1c_x3c", "x2c_x3c")

for (i in 1:6) {
  vr <- as.numeric(resultados_df[i,-(1:3)])   # valor real a estimar
  
  des_dfp <- resultados_df[-i,]               # tabla con valores disponibles
  ve <- numeric(n)                     # vector para guardar predicciones
  
  # definición de los 7 tratamientos del simplex
  tratamientos <- list(
    c(1, 0, 0),
    c(0.5, 0.5, 0),
    c(0, 1, 0),
    c(0, 0.5, 0.5),
    c(0, 0, 1),
    c(0.5, 0, 0.5),
    c(1/3, 1/3, 1/3, 1/3, 1/3, 1/3, 1/3, 1/3, 1/3))
  
    for (j in 1:n) {
        # fórmula cuadrática dinámica: 
        #yi ~ x1 + x2 + I(x1^2) + I(x2^2) + I(x1*x2)

        f <- as.formula(paste0("y", j, 
                               " ~ x1 + x2 + I(x1^2) + I(x2^2) + I(x1*x2)"))

        # ajustar modelo
        mod[[j]] <- lm(f, data = des_dfp)# modelo sin el valor a estimar
        
        # obtener coeficientes transformados 
        a <- coefficients(mod[[j]])
        
        # Paso a canónicos (siguiendo tu función mlmc)
        a0  <- a["(Intercept)"]
        a1  <- a["x1"]
        a2  <- a["x2"]
        a11 <- a["I(x1^2)"]
        a22 <- a["I(x2^2)"]
        a12 <- a["I(x1 * x2)"]
        
        ## Transformación a coeficientes canónicos ---
        x1c <-  a0 + a1 + a11
        x2c <-  a0 + a2 + a22
        x3c <-  a0
        x1c_x2c <-  a12 - a11 - a22
        x1c_x3c <-  -a11
        x2c_x3c <-  -a22
        
        coefs[j, ] <- c(x1c, x2c, x3c, x1c_x2c, x1c_x3c, x2c_x3c)
        
        # armar newdata según tratamiento sel
        newdata <- data.frame(matrix(tratamientos[[i]], nrow = 1))
        x1 <- newdata[,1]; x2 <- newdata[,2]; x3 <- newdata[,3]
        
        # predecir
        ve[j] <- coefs[j,"x1c"]*x1 + coefs[j,"x2c"]*x2 + coefs[j,"x3c"]*x3 +
          coefs[j,"x1c_x2c"]*x1*x2 + coefs[j,"x1c_x3c"]*x1*x3 +
          coefs[j,"x2c_x3c"]*x2*x3}

  abserror421[,i] <- (abs(vr - ve))         
  errorcua421[,i] <- (vr - ve)^2
  
  resumenli[9, i+2] <- round(mean(abserror421[,i]),2)
  resumenli[10, i+2] <- round(sqrt(mean(errorcua421[,i])),2)
  }

5.2 Modelo cuadrático

Se emplea la misma función descrita anteriormente, modificando el argumento a mod = 2, así:

rm(ymat)
ymat2 <- matrix(NA, nrow = nrow(des), ncol = n)

for (i in 1:n) {
    ymat2[, i] <- gen_scheffe(des, 
                             sd = 1,
                             mod = 2)
  }
  colnames(ymat2) <- paste0("y", 1:n)
  resultados_df <- cbind(des, as.data.frame(ymat2)) 
  res <- 0.82 + (resultados_df$y9/10)
  res

[1] 1.8662513 0.9004555 0.2291747 1.1170002 1.7076118 1.4702207 1.1167179
[8] 1.1241400 1.4809150

Se simulan 1000 modelos generados a partir de un modelo cuadrático canónico de Scheffé. A continuación, se presenta uno de ellos:

     
      coefficients  Std.err    t.value        Prob
x1       3.4917656 1.104263  3.1620773 0.050789711
x2      -7.1187491 1.103061 -6.4536290 0.007546374
x3      -3.1815329 1.103061 -2.8842754 0.063307769
x2:x1    1.4273828 4.846615  0.2945113 0.787570499
x3:x1   -0.7669499 4.846615 -0.1582445 0.884316180
x2:x3   19.6271745 4.834877  4.0594980 0.026944830
     
Residual standard error:  1.109706  on  3 degrees of freedom 
Corrected Multiple R-squared:  0.9477758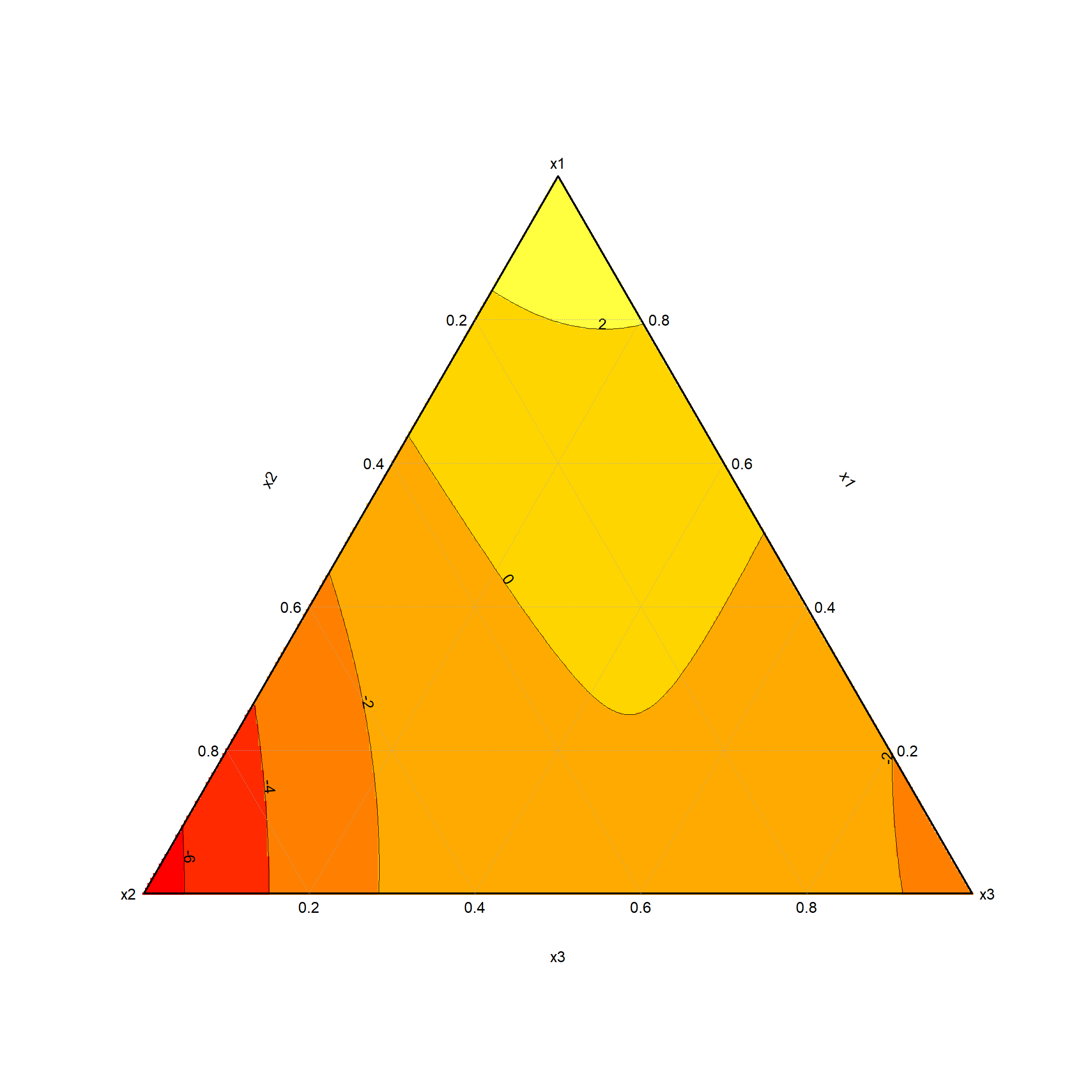

Figura 5.2: Diseño simplex con centroide simulado con modelo cuadrático - Gráfica de contorno

La imputación se lleva a cabo para cada uno de los métodos empleando los mismos procedimientos y códigos utilizados previamente en el modelo lineal.

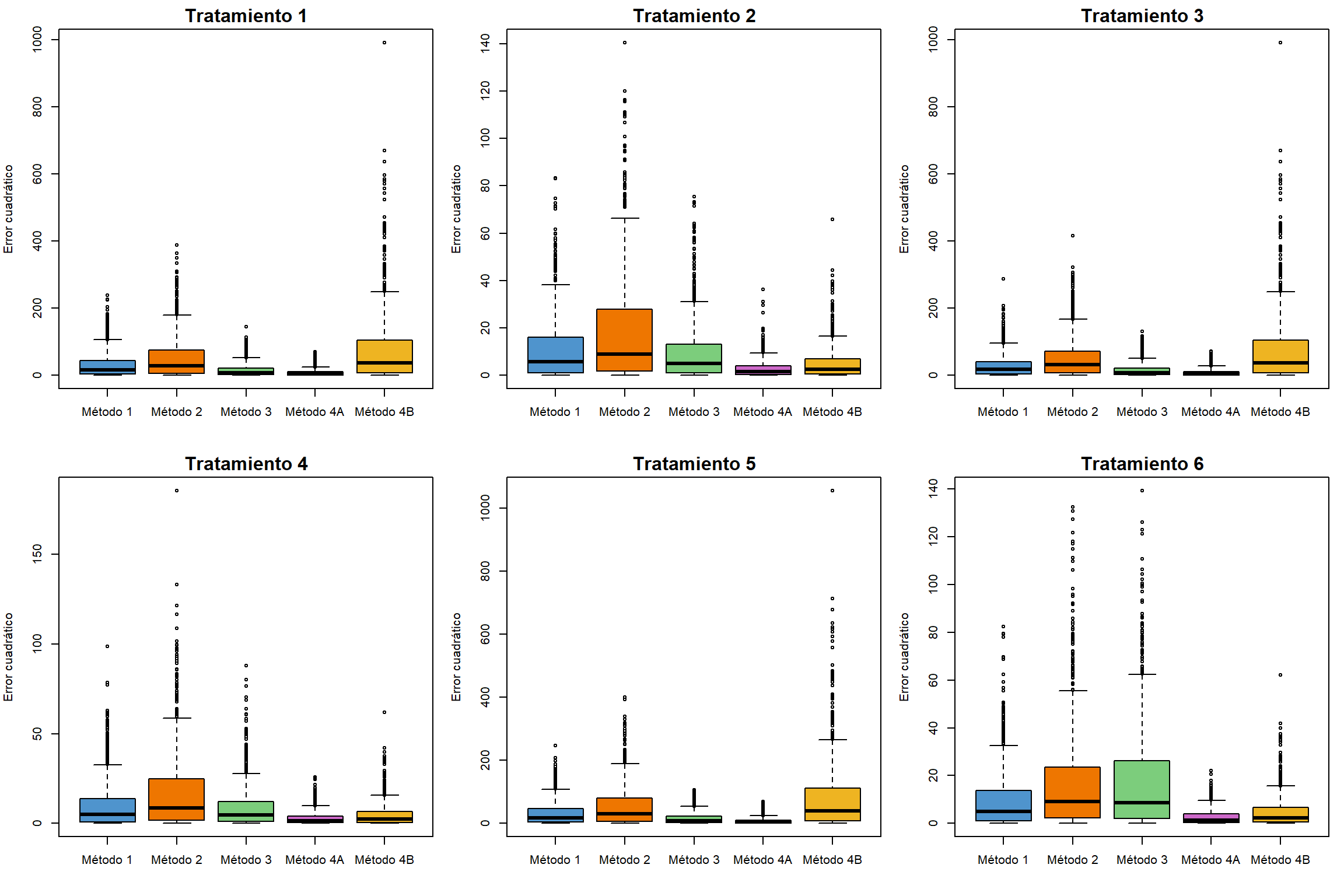
6 Resultados

6.1 Modelo lineal

Método de imputación	Métricas de error	T 1	T 2	T 3	T 4	T 5	T 6
Método 1 Promedio general	EAM	4.20	2.37	4.35	2.21	4.56	2.27
	RECM	5.21	2.92	5.33	2.73	5.54	2.81
Método 2 Promedio entre similares	EAM	5.55	3.11	5.80	2.91	6.09	3.00
	RECM	6.89	3.80	7.07	3.59	7.38	3.70
Método 3 Promedio entre vecinos más cercanos	EAM	2.92	2.28	2.99	2.13	3.14	3.19
	RECM	3.63	2.85	3.67	2.64	3.85	3.86
Método 4 - I Modelo lineal	EAM	1.37	0.92	1.29	0.86	1.33	0.94
	RECM	1.71	1.17	1.62	1.10	1.64	1.18
Método 4 - II Modelo cuadrático	EAM	7.03	1.81	7.03	1.76	7.25	1.76
	RECM	8.84	2.28	8.84	2.21	9.11	2.21

Tabla 6.1: Resumen de los EAM y RECM según el método de imputación para datos generados por modelo lineal canónico de Scheffé

6.2 Modelo cuadrático

Método de imputación	Métricas de error	T 1	T 2	T 3	T 4	T 5	T 6
Método 1 Promedio general	EAM	4.54	2.66	4.53	2.54	4.64	2.57
	RECM	5.58	3.29	5.47	3.16	5.62	3.15
Método 2 Promedio entre similares	EAM	6.00	3.48	6.00	3.36	6.09	3.41
	RECM	7.33	4.28	7.21	4.15	7.39	4.16
Método 3 Promedio entre vecinos más cercanos	EAM	3.18	2.55	3.18	2.43	3.26	3.43
	RECM	3.95	3.13	3.88	3.00	3.97	4.20
Método 4 - I Modelo lineal	EAM	2.19	1.43	2.34	1.37	2.25	1.34
	RECM	2.70	1.75	2.88	1.71	2.77	1.63
Método 4 - II Modelo cuadrático	EAM	7.07	1.82	7.07	1.77	7.29	1.77
	RECM	8.82	2.27	8.82	2.20	9.09	2.20

Tabla 6.2: Resumen de los EAM y RECM según el método de imputación para datos generados por modelo cuadrático canónico de Scheffé

7 Anexos

Tratamiento inicial	Tratamiento final	Distancia	Clasificación
1	2	0.50	1
1	6	0.50	1
1	7	0.67	2
1	4	0.86	2
1	3	1.00	3
1	5	1.00	3
2	7	0.33	1
2	1	0.50	2
2	3	0.50	2
2	4	0.50	2
2	6	0.50	2
2	5	0.86	3
3	2	0.50	1
3	4	0.50	1
3	7	0.67	2
3	6	0.86	2
3	1	1.00	3
3	5	1.00	3
4	7	0.33	1
4	2	0.50	2
4	3	0.50	2
4	5	0.50	2
4	6	0.50	2
4	1	0.86	3
5	4	0.50	1
5	6	0.50	1
5	7	0.67	2
5	2	0.86	2
5	1	1.00	3
5	3	1.00	3
6	1	0.50	1
6	2	0.50	1
6	7	0.67	2
6	4	0.86	2
6	3	1.00	3
6	5	1.00	3
7	2	0.33	1
7	4	0.33	1
7	6	0.33	1
7	1	0.67	2
7	3	0.67	2
7	5	0.67	2

Tabla 7.1: Caracterización de los tratamientos experimentales del diseño simplex con centroide

Wongoutong, Chantha. 2022. «Imputation methods for missing response values in the three parts of a central composite design with two factors». Journal of Statistical Computation and Simulation 92 (11): 2273-89.