8 Replicación en R de caso de estudio: Rahamathulla et al. (2022)

2³ factorial design and optimization of effervescent floating matrix tablet of neratinib

9 Artículo de estudio

Rahamathulla et al. (2022) presenta en su artículo “2³ factorial design and optimization of effervescent floating matrix tablet of neratinib”, la formulación de una tableta con sistema de liberación flotante de neratinib, empleada en el tratamiento del cáncer de mama. Este fármaco presenta una baja solubilidad en agua a pH elevado, lo que limita su eficacia terapéutica y, en consecuencia, su biodisponibilidad. Por esta razón, es preferible que la absorción del fármaco se produzca en el estómago, donde el pH es bajo. Sin embargo, la permanencia del fármaco en el estómago se ve afectada por factores como el vaciado y la motilidad gástrica, entre otros. Para superar esta limitación, se diseñó una tableta con un sistema de liberación flotante, con el objetivo de prolongar el tiempo de residencia gástrica y, de este modo, incrementar su biodisponibilidad.

Para el desarrollo de la matriz se empleó un diseño factorial 2³ con puntos centrales, en el cual se evaluaron como factores las concentraciones de los excipientes hidroxipropilmetilcelulosa, carbopol 940 y celulosa microcristalina. El artículo presenta la evaluación de varias variables respuesta; sin embargo, en este ejercicio solo se tendrá en cuenta el índice de Carr (CARR) y la friabilidad (FRIAB).

Nota

Véase “Guía para la implementación de diseños experimentales en la industria farmacéutica” para una explicación detallada de los cálculos presentados.

Librerías requeridas: FrF2, dplyr, knitr, flextable, ggplot2, gridExtra

10 Factores evaluados

Variables	Nivel (-1)	Nivel (0)	Nivel (1)
Hidroxipropilmetilcelulosa (HPMC)	25 mg	37.5 mg	50 mg
Carbopol 940 (CARB)	25 mg	37.5 mg	50 mg
Celulosa microcristalina (MCC)	15 mg	20 mg	25 mg

Tabla 10.1: Tabla 1. Factores y niveles considerados por Rahamathulla et al. (2022)

11 Simulación de respuestas

El artículo de (Rahamathulla et al. 2022) reporta únicamente el valor promedio de las tres réplicas junto con su desviación estándar, , por lo que se requiere simular los datos individuales. Para este propósito, se construyó la función simuesblo, disponible en el archivo funciones.R del repositorio ncortes/Disexp_Industria_Farmaceutica en GitHub (funcionesR?).

Código

# Respuestas reportadas como promedio y desviación estándar

carr_mean <- c(12.71, 13.87, 14.20,  5.28, 10.79,  8.00,  6.00, 10.20, 3.00)
carr_sd   <- c(0.91,  1.03,  1.22,  2.09,  2.04,  1.51,  1.33,  0.59,  1.02)
CARR <- as.vector(simuesblo(carr_mean, carr_sd, 3, 2))

Los valores simulados para el índice de Carr son: 12.2, 13.94, 14.76, 4.35, 11.61, 10.7, 6.93, 10.07, 2.36, 12.5, 14, 12.66, 7.84, 11.02, 8.75, 5.37, 9.59, 1.28, 14.13, 15.64, 13.36, 6.03, 9.66, 5.03, 4.58, 9.77, 3.85

12 Diseño factorial completo 2³ con puntos centrales

Código

# Diseño de variables codificadas
dis1_cod <- data.frame(
  TRAT    = rep(paste("TRAT", seq(1,9)),3),
  HPMC    = rep(c(1, -1, -1,  1,  1, -1,  0,  -1,  1),3),
  CARB = rep(c(1, -1, -1,  1, -1,  1,  0,   1,  -1),3),
  MCC     = rep(c(1,  1, -1, -1, -1, -1,  0,   1,  1),3),
  CARR)

# Diseño de variables naturales

dis1_nat <- data.frame(
  TRAT_    = rep(paste("TRAT", seq(1,9)),3),
  HPMC_    = rep(c(50, 25, 25, 50, 50, 25, 37.5, 25, 50), 3),
  CARB_ = rep(c(50, 25, 25, 50, 25, 50, 37.5, 50, 25), 3),
  MCC_     = rep(c(25, 25, 15, 15, 15, 15, 20,   25, 25), 3),
  CARR)

TRATAMIENTOS	HPMC(c)	CARB(c)	MCC(c)	HPMC(n)	CARB(n)	MCC(n)	CARR
TRAT 1	1	1	1	50.0	50.0	25	12.20
TRAT 2	-1	-1	1	25.0	25.0	25	13.94
TRAT 3	-1	-1	-1	25.0	25.0	15	14.76
TRAT 4	1	1	-1	50.0	50.0	15	4.35
TRAT 5	1	-1	-1	50.0	25.0	15	11.61
TRAT 6	-1	1	-1	25.0	50.0	15	10.70
TRAT 7	0	0	0	37.5	37.5	20	6.93
TRAT 8	-1	1	1	25.0	50.0	25	10.07
TRAT 9	1	-1	1	50.0	25.0	25	2.36
TRAT 1	1	1	1	50.0	50.0	25	12.50
TRAT 2	-1	-1	1	25.0	25.0	25	14.00
TRAT 3	-1	-1	-1	25.0	25.0	15	12.66
TRAT 4	1	1	-1	50.0	50.0	15	7.84
TRAT 5	1	-1	-1	50.0	25.0	15	11.02
TRAT 6	-1	1	-1	25.0	50.0	15	8.75
TRAT 7	0	0	0	37.5	37.5	20	5.37
TRAT 8	-1	1	1	25.0	50.0	25	9.59
TRAT 9	1	-1	1	50.0	25.0	25	1.28
TRAT 1	1	1	1	50.0	50.0	25	14.13
TRAT 2	-1	-1	1	25.0	25.0	25	15.64
TRAT 3	-1	-1	-1	25.0	25.0	15	13.36
TRAT 4	1	1	-1	50.0	50.0	15	6.03
TRAT 5	1	-1	-1	50.0	25.0	15	9.66
TRAT 6	-1	1	-1	25.0	50.0	15	5.03
TRAT 7	0	0	0	37.5	37.5	20	4.58
TRAT 8	-1	1	1	25.0	50.0	25	9.77
TRAT 9	1	-1	1	50.0	25.0	25	3.85
(c): notación codificada; (n): notación natural

Tabla 12.1: Tratamientos para la evaluación de las variables respuesta en tabletas de Neratinib

12.1 Indice de Carr

12.1.1 Modelo de regresión

Código

mod1 <- lm(CARR~HPMC*CARB*MCC, dis1_cod)
summary(mod1)


Call:
lm.default(formula = CARR ~ HPMC * CARB * MCC, data = dis1_cod)

Residuals:
    Min      1Q  Median      3Q     Max 
-4.7526 -0.5551  0.2432  1.1816  3.0032 

Coefficients:
              Estimate Std. Error t value Pr(>|t|)    
(Intercept)     9.3326     0.4038  23.111 2.27e-15 ***
HPMC           -1.7267     0.4283  -4.031 0.000713 ***
CARB           -0.5492     0.4283  -1.282 0.215211    
MCC             0.1483     0.4283   0.346 0.732909    
HPMC:CARB       1.9883     0.4283   4.642 0.000178 ***
HPMC:MCC       -0.4975     0.4283  -1.162 0.259811    
CARB:MCC        1.9817     0.4283   4.627 0.000184 ***
HPMC:CARB:MCC   1.8025     0.4283   4.208 0.000476 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 2.098 on 19 degrees of freedom
Multiple R-squared:  0.8081,    Adjusted R-squared:  0.7375 
F-statistic: 11.43 on 7 and 19 DF,  p-value: 1.219e-05

12.1.2 Verificación de supuestos

Código

# Residuos del modelo
residuales <- mod1$residuals

# Prueba de homogeneidad de varianzas
  modx <- lm(CARR~TRAT, dis1_cod)
  residualesx <- residuals(modx)
  bt <- bartlett.test(residualesx~TRAT, data=dis1_cod)

# Prueba de normalidad de Kolmogorov-Smirnov
ks <- ks.test(residuales,"pnorm",mean(residuales), sd(residuales))

# Prueba de normalidad de Shapiro-Wilk
sp <- shapiro.test(residuales)

Pruebas	p-valor	Interpretación
Prueba de bartlett	0.3681	Los residuales son homocedásticos
Kolmogorov-Smirnov	0.5120	Los residuales son normales
Shapiro-Wilk	0.0501	Los residuales son normales

Tabla 12.2: Análisis de supuestos de los residuales estandarizados par ael índice de Carr

Código

anova(mod1)

Analysis of Variance Table

Response: CARR
              Df Sum Sq Mean Sq F value    Pr(>F)    
HPMC           1 71.553  71.553 16.2515 0.0007133 ***
CARB           1  7.238   7.238  1.6439 0.2152110    
MCC            1  0.528   0.528  0.1199 0.7329086    
HPMC:CARB      1 94.883  94.883 21.5503 0.0001777 ***
HPMC:MCC       1  5.940   5.940  1.3492 0.2598107    
CARB:MCC       1 94.248  94.248 21.4061 0.0001840 ***
HPMC:CARB:MCC  1 77.976  77.976 17.7103 0.0004761 ***
Residuals     19 83.655   4.403                      
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

12.1.3 Graficos de interacción

Código

#jpeg("mi_grafico.jpg", width = 1400, height = 800, res = 150)
dis1_cod2 <- subset(dis1_cod, CARB %in% c(-1, 1))
dis1_cod2$CARB <- factor(dis1_cod2$CARB)

p1 <- ggplot(dis1_cod2, aes(x = HPMC, y = CARR, group = CARB, color = CARB)) +
  stat_summary(fun = mean, geom = "line", linewidth = 1.2) +
  stat_summary(fun = mean, geom = "point", size = 3) +
  scale_x_continuous(breaks = c(-1, 1)) +
  scale_color_manual(values = c("blue", "black")) +
  labs(x = "HPMC", y = "CARR", color = "CARB") +
  theme_minimal()

dis1_cod2 <- subset(dis1_cod, CARB %in% c(-1, 1))
dis1_cod2$CARB <- factor(dis1_cod2$CARB)

p2 <- ggplot(dis1_cod2, aes(x = MCC, y = CARR, group = CARB, color = CARB)) +
  stat_summary(fun = mean, geom = "line", linewidth = 1.2) +
  stat_summary(fun = mean, geom = "point", size = 3) +
  scale_x_continuous(breaks = c(-1, 1)) +
  scale_color_manual(values = c("blue", "black")) +
  labs(x = "MCC", y = "CARR", color = "CARB") +
  theme_minimal()

dis1_cod2 <- subset(dis1_cod, MCC %in% c(-1, 1))
dis1_cod2$MCC <- factor(dis1_cod2$MCC)

p3 <- ggplot(dis1_cod2, aes(x = HPMC, y = CARR, group = MCC, color = MCC)) +
  stat_summary(fun = mean, geom = "line", linewidth = 1.2) +
  stat_summary(fun = mean, geom = "point", size = 3) +
  scale_x_continuous(breaks = c(-1, 1)) +
  scale_color_manual(values = c("blue", "black")) +
  labs(x = "HPMC", y = "CARR", color = "MCC") +
  theme_minimal()

grid.arrange(p1, p2, p3, ncol = 3)
#dev.off()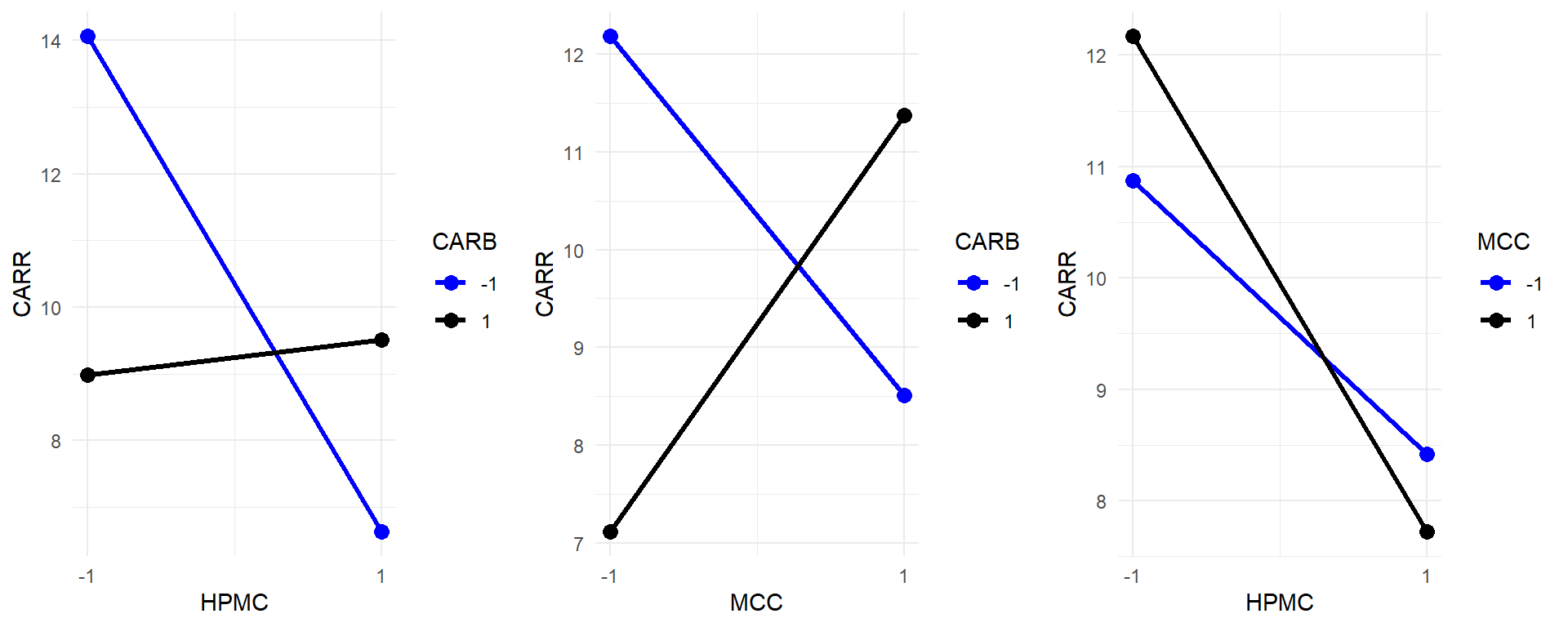

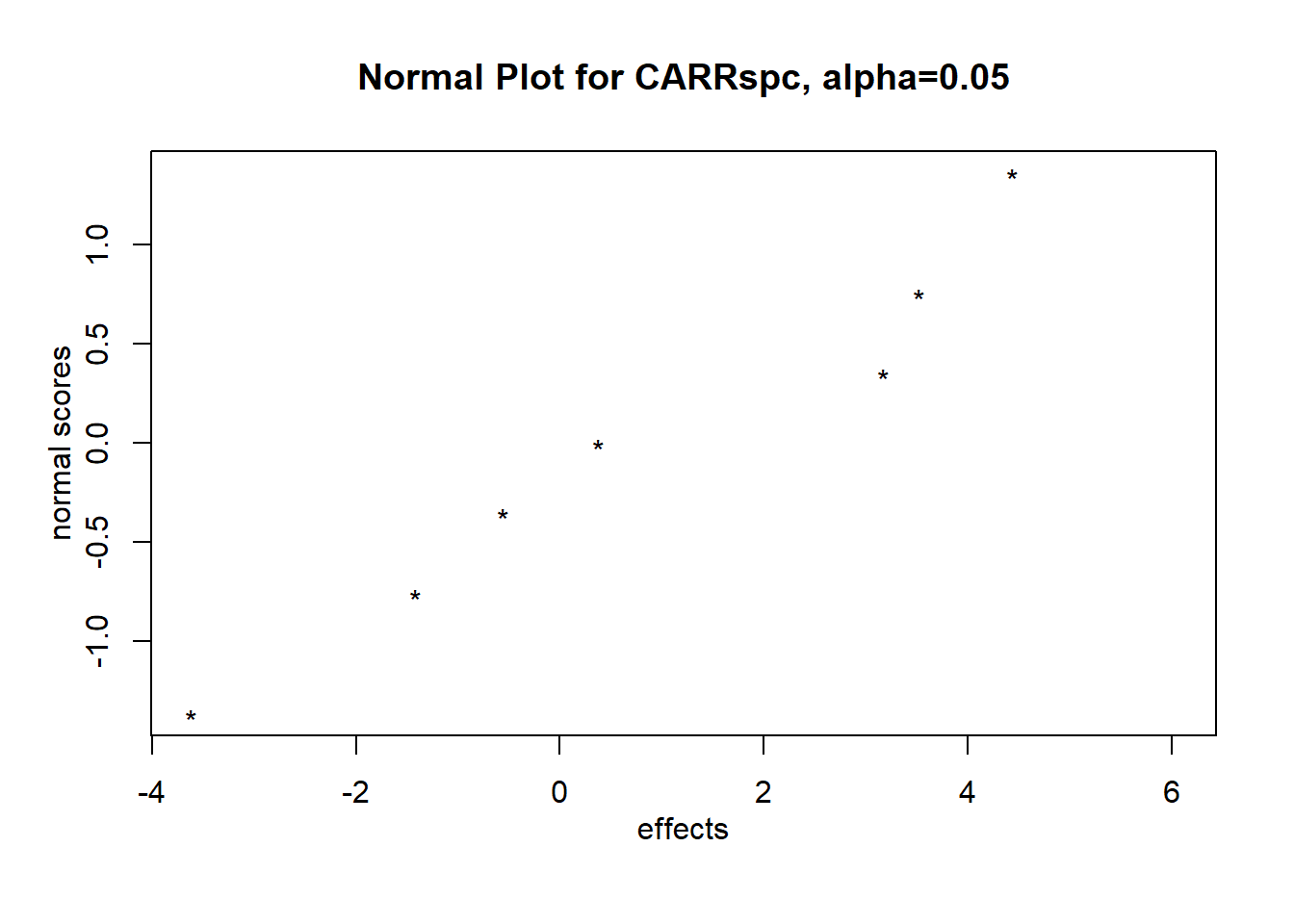
13 Diseño factorial completo 2³ no replicado y sin puntos centrales

Para construir un diseño factorial completo 2³ no replicado y sin puntos centrales, se eliminan las filas correspondientes al punto central (TRAT 7) y se incorpora directamente la variable respuesta CARR, tal como fue reportada en el artículo, sin realizar simulación de réplicas.

Código

# Diseño de variables codificadas
CARRspc <- carr_mean[-7]
dis2_cod <- data.frame(
  TRAT    = paste("TRAT", seq(1,8)),
  HPMC    = c(1, -1, -1,  1,  1, -1,  -1,  1),
  CARB = c(1, -1, -1,  1, -1,  1,   1,  -1),
  MCC     = c(1,  1, -1, -1, -1, -1,   1,  1),
  CARRspc)

# Diseño de variables naturales

dis2_nat <- data.frame(
  TRAT    = paste("TRAT", seq(1,8)),
  HPMC_    = c(50, 25, 25, 50, 50, 25, 25, 50),
  CARB_ = c(50, 25, 25, 50, 25, 50, 50, 25),
  MCC_     = c(25, 25, 15, 15, 15, 15, 25, 25),
  CARRspc)

TRATAMIENTOS	HPMC(c)	CARB(c)	MCC(c)	HPMC(n)	CARB(n)	MCC(n)	CARR
TRAT 1	1	1	1	50	50	25	12.71
TRAT 2	-1	-1	1	25	25	25	13.87
TRAT 3	-1	-1	-1	25	25	15	14.20
TRAT 4	1	1	-1	50	50	15	5.28
TRAT 5	1	-1	-1	50	25	15	10.79
TRAT 6	-1	1	-1	25	50	15	8.00
TRAT 7	-1	1	1	25	50	25	10.20
TRAT 8	1	-1	1	50	25	25	3.00
(c): notación codificada; (n): notación natural

Tabla 13.1: Tratamientos para la evaluación de las variables respuesta en tabletas de Neratinib en un diseño factorrial completo 2³ no replicado y sin puntos centrales

Código

mod2 <- lm(CARRspc~HPMC*CARB*MCC, dis2_cod)
DanielPlot(mod2)

14 Diseño factorial completo 2³ no replicado con puntos centrales

Para construir un diseño factorial completo 2³ no replicado con puntos centrales, se incorpora directamente la variable respuesta CARR, tal como fue reportada en el artículo, sin realizar simulación de réplicas.

Código

# Diseño de variables codificadas
CARRmean <- carr_mean
dis3_cod <- data.frame(
  TRAT    = paste("TRAT", seq(1,9)),
  HPMC    = c(1, -1, -1,  1,  1, -1, 0, -1,  1),
  CARB = c(1, -1, -1,  1, -1,  1, 0,  1,  -1),
  MCC     = c(1,  1, -1, -1, -1, -1,  0, 1,  1),
  CARRmean)

# Diseño de variables naturales

dis3_nat <- data.frame(
  TRAT    = paste("TRAT", seq(1,9)),
  HPMC_    = c(50, 25, 25, 50, 50, 25, 37.5, 25, 50),
  CARB_ = c(50, 25, 25, 50, 25, 50, 37.5, 50, 25),
  MCC_     = c(25, 25, 15, 15, 15, 15, 20, 25, 25),
  CARRmean)

TRATAMIENTOS	HPMC(c)	CARB(c)	MCC(c)	HPMC(n)	CARB(n)	MCC(n)	CARR
TRAT 1	1	1	1	50.0	50.0	25	12.71
TRAT 2	-1	-1	1	25.0	25.0	25	13.87
TRAT 3	-1	-1	-1	25.0	25.0	15	14.20
TRAT 4	1	1	-1	50.0	50.0	15	5.28
TRAT 5	1	-1	-1	50.0	25.0	15	10.79
TRAT 6	-1	1	-1	25.0	50.0	15	8.00
TRAT 7	0	0	0	37.5	37.5	20	6.00
TRAT 8	-1	1	1	25.0	50.0	25	10.20
TRAT 9	1	-1	1	50.0	25.0	25	3.00
(c): notación codificada; (n): notación natural

Tabla 14.1: Tratamientos para la evaluación de las variables respuesta en tabletas de Neratinib en un diseño factorrial completo 2³ no replicado con puntos centrales

Código

mod3 <- lm(CARRmean~HPMC*CARB*MCC, dis3_cod)
summary(mod3)


Call:
lm.default(formula = CARRmean ~ HPMC * CARB * MCC, data = dis3_cod)

Residuals:
      1       2       3       4       5       6       7       8       9 
 0.4174  0.4174  0.4174  0.4174  0.4174  0.4174 -3.3389  0.4174  0.4174 

Coefficients:
              Estimate Std. Error t value Pr(>|t|)  
(Intercept)     9.3389     1.1805   7.911    0.080 .
HPMC           -1.8112     1.2521  -1.447    0.385  
CARB           -0.7087     1.2521  -0.566    0.672  
MCC             0.1888     1.2521   0.151    0.905  
HPMC:CARB       1.7587     1.2521   1.405    0.394  
HPMC:MCC       -0.2787     1.2521  -0.223    0.861  
CARB:MCC        2.2188     1.2521   1.772    0.327  
HPMC:CARB:MCC   1.5863     1.2521   1.267    0.425  
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 3.541 on 1 degrees of freedom
Multiple R-squared:  0.902, Adjusted R-squared:  0.216 
F-statistic: 1.315 on 7 and 1 DF,  p-value: 0.5879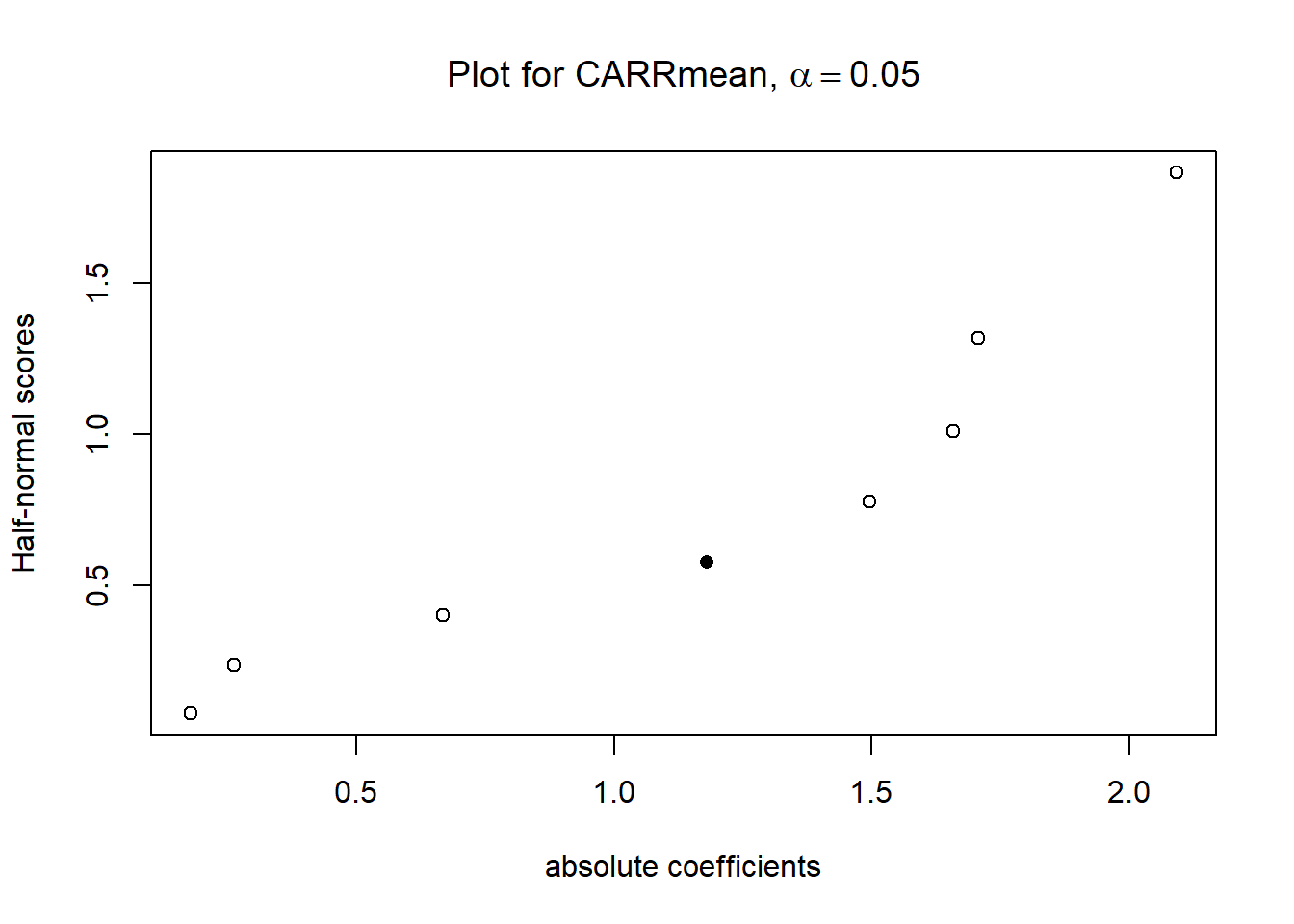

Código

graf <- suppressMessages(halfnormal(mod3, alpha = 0.05, plot=TRUE, method="Lenth"))

Código

signif <- graf$signif
signif

character(0)

Rahamathulla, Mohamed, Umme Hani, Ali Alqahtani, Gangadharappa HV, Yasmin Begum M, Mohammed Jafar, Riyaz Ali M Osmani, Kumarappan Chidambaram, Afrasim Moin, y SJ Shankar. 2022. «23 factorial design and optimization of effervescent floating matrix tablet of neratinib». Journal of Pharmaceutical Innovation 17 (4): 1451-62.

Volver arriba