11 Replicación en R de caso de estudio: Yüksel et al. (2007)

Lubricant Efficiency of Magnesium Stearate in Direct Compressible Powder Mixtures Comprising Cellactose® 80 and Pyridoxine Hydrochloride, artículo escrito por Yüksel et al. (2007)

12 Artículo de estudio

El propósito del artículo de Yüksel et al. (2007), Lubricant Efficiency of Magnesium Stearate in Direct Compressible Powder Mixtures Comprising Cellactose® 80 and Pyridoxine Hydrochloride fue evaluar el impacto del estearato de magnesio como lubricante sobre las propiedades de las tabletas elaboradas con Cellactose®80 y clorhidrato de piridoxina. Hay varios trabajos relacionados con el mismo tema, en particular se invita a revisar el trabajo publicado por Kikuta y Kitamori (1994). En este caso, el diseño de experimentos utilizado es un Diseño completamente aleatorizado donde los resultados obtenidos para la prueba de disolución son analizados mediante un análisis de varianza (ANOVA) por tratamiento. Aunque el artículo proporciona la desviación estándar de cada tratamiento, se generaron valores simulados únicamente con fines ilustrativos.

Nota

Véase “Guía para la implementación de diseños experimentales en la industria farmacéutica” para una explicación detallada de los cálculos presentados.

Librerías requeridas: dplyr, flextable, car, nortest, ggplot2

13 Simulación de respuestas

El artículo de Yüksel et al. (2007) reporta el valor promedio de las tres réplicas junto con su desviación estándar, por lo que se requiere simular los datos individuales. Para este propósito, se construyó la función simuesblo, disponible en el archivo funciones.R del repositorio ncortes/Disexp_Industria_Farmaceutica en GitHub (funcionesR?).

Código

# Disolución
DIS_mean <- c(86.6, 86.1, 37.6, 93.1, 84.8, 41.6, 87.8, 89.0, 28.9)
DIS_sd <- rnorm(9,2.5,0.1)       #Desviaciones estandar sugeridas
DIS <- as.vector(simuesblo(DIS_mean, DIS_sd, 3, 2))

Los valores simulados para la disolución son: 85.15, 86.27, 38.77, 92, 85.76, 46.16, 89.55, 88.48, 27.3, 86, 86.42, 34.38, 96.12, 85.07, 42.87, 86.62, 86.56, 24.58, 90.64, 90.3, 35.85, 93.99, 83.46, 36.58, 85.13, 87.27, 31.04

TRAT	R1	R2	R3
T1	85.15	86.00	90.64
T2	86.27	86.42	90.30
T3	38.77	34.38	35.85
T4	92.00	96.12	93.99
T5	85.76	85.07	83.46
T6	46.16	42.87	36.58
T7	89.55	86.62	85.13
T8	88.48	86.56	87.27
T9	27.30	24.58	31.04

Tabla 13.1: Réplicas simuladas a partir de las medias por tratamiento reportadas en (Yüksel et al. 2007)

14 Modelo de regresión

Código

# Diseño
dis<- data.frame(TRAT=c(rep(paste0("T", 1:9),3)), DIS)
mod <- lm(DIS ~ TRAT, data = dis)

15 ANOVA

Código

anova(mod)

Analysis of Variance Table

Response: DIS
          Df  Sum Sq Mean Sq F value    Pr(>F)    
TRAT       8 17158.3  2144.8   297.9 < 2.2e-16 ***
Residuals 18   129.6     7.2                      
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

16 Verificación de supuestos

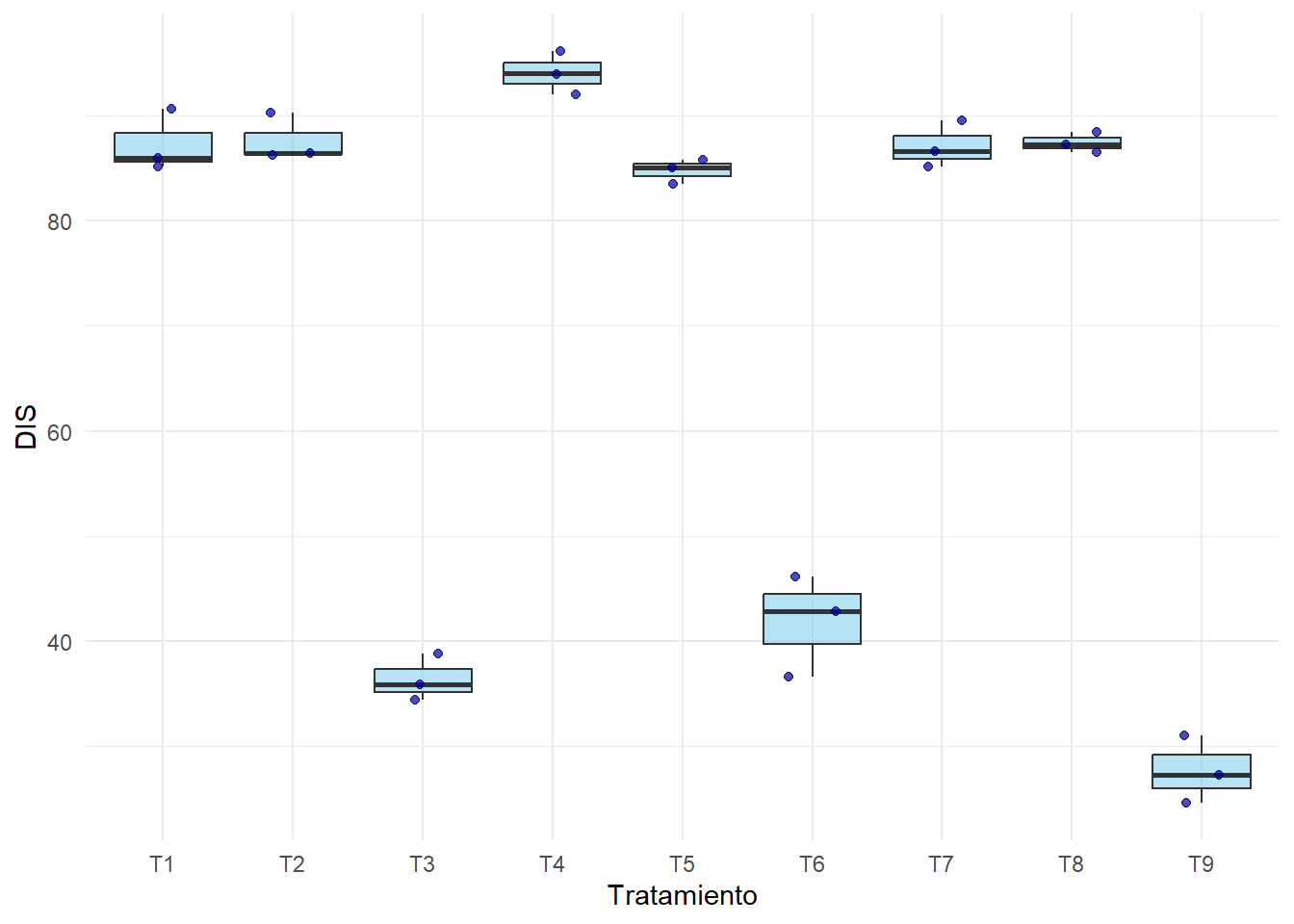
Análisis descriptivo de los tratamientos:

Código

ggplot(dis, aes(x = TRAT, y = DIS)) +
  geom_boxplot(fill = "skyblue", alpha = 0.6) +
  geom_jitter(width = 0.2, alpha = 0.7, color = "darkblue") +
  labs(x = "Tratamiento",
       y = "DIS") +
  theme_minimal()

Figura 16.1: Boxplot de los tratamientos evaluados en (Yüksel et al. 2007)

Código

# Residuos del modelo
residuales <- mod$residuals

# Prueba de homogeneidad de varianzas
bt <- bartlett.test(residuales~TRAT, data=dis)

# Prueba de normalidad de Kolmogorov-Smirnov
ks <- ks.test(residuales,"pnorm",mean(residuales), sd(residuales))

# Prueba de normalidad de Shapiro-Wilk
sp <- shapiro.test(residuales)

Pruebas	Estadístico	p-valor	Interpretación
test de bartlett	5.8750	0.6612	Los residuales son homocedásticos
Kolmogorov-Smirnov	0.1009	0.9204	Los residuales son normales
Shapiro-Wilk	0.9721	0.6590	Los residuales son normales

Tabla 16.1: Análisis de supuestos de los residuales estandarizados

Kikuta, Jun-Ichi, y Nobuyuki Kitamori. 1994. «Effect of mixing time on the lubricating properties of magnesium stearate and the final characteristics of the compressed tablets». Drug development and industrial pharmacy 20 (3): 343-55.

Yüksel, Nilüfer, Berna Türkmen, Aslıhan H Kurdoğlu, BERRİN Başaran, Jülide Erkin, y Tamer Baykara. 2007. «Lubricant efficiency of magnesium stearate in direct compressible powder mixtures comprising cellactose 80 and pyridoxine hydrochloride». Fabad J. Pharm. Sci 32: 173-83.

Volver arriba