12 Lewis 2001

Nota

El presente documento corresponde a un apartado del trabajo titulado “Guía para la implementación de diseños experimentales en la industria farmacéutica”, presentado por Nathalia Cortés Duque como requisito para optar al título de Magíster en Ciencias - Estadística de la Universidad Nacional de Colombia.

Código

library(FrF2)
library(flextable)
library(tidyverse)

12.1 Ejemplo 1: Drill Data

Este es un diseño factorial \(2^4\) sin réplicas. El diseño es analizado usando tres modelos de regresión:

Mínimos cuadrados ordinarios con los datos originales
Mínimos cuadrados ordinarios después de transformar logarítmicamente los datos originales
Modelo Lineal Generalizado asumiendo que la variable respuesta sigue una distribución Gamma y usando link de enlace logaritmo.

El diseño es el siguiente:

Código

# Diseño
dis <- FrF2(nruns = 16, nfactors = 4,
            factor.names = c("A", "B", "C", "D"),
            randomize = FALSE)

creating full factorial with 16 runs ...

Código

# Respuesta obtenida
y <- c(1.68, 1.98, 3.28, 3.44, 4.98, 5.7, 9.97, 9.07, 2.07, 2.44, 4.09, 4.53, 7.77, 9.43, 11.75, 16.3)

dis_y <- add.response(dis, y)

12.1.1 Mínimos Cuadrados Ordinarios

Usando los datos originales, se ajusta el modelo lineal saturado (con todos los factores e interacciones).

Código

mod1 <- lm(y ~ A*B*C*D, data=dis_y)
summary(mod1)


Call:
lm.default(formula = y ~ A * B * C * D, data = dis_y)

Residuals:
ALL 16 residuals are 0: no residual degrees of freedom!

Coefficients:
            Estimate Std. Error t value Pr(>|t|)
(Intercept)  6.15500        NaN     NaN      NaN
A1           0.45625        NaN     NaN      NaN
B1           1.64875        NaN     NaN      NaN
C1           3.21625        NaN     NaN      NaN
D1           1.14250        NaN     NaN      NaN
A1:B1        0.07500        NaN     NaN      NaN
A1:C1        0.29750        NaN     NaN      NaN
B1:C1        0.75250        NaN     NaN      NaN
A1:D1        0.42125        NaN     NaN      NaN
B1:D1        0.22125        NaN     NaN      NaN
C1:D1        0.79875        NaN     NaN      NaN
A1:B1:C1     0.08375        NaN     NaN      NaN
A1:B1:D1     0.29500        NaN     NaN      NaN
A1:C1:D1     0.37750        NaN     NaN      NaN
B1:C1:D1     0.09000        NaN     NaN      NaN
A1:B1:C1:D1  0.26875        NaN     NaN      NaN

Residual standard error: NaN on 0 degrees of freedom
Multiple R-squared:      1, Adjusted R-squared:    NaN 
F-statistic:   NaN on 15 and 0 DF,  p-value: NA

Dado que el modelo es saturado y no tiene réplicas, cada observación es predicha de forma perfecta por el modelo, no hay grados de libertad y por lo tanto no es posible calcular la varianza residual ni los p-valores asociados a los efectos de los factore y sus interacciones.

Aún así, es posible calcular los efectos estimados a partir del modelo de regresión ajustado. Si \(\beta\) es el coeficiente estimado del \(i\)-ésimo término del modelo de regresión, entonces su efecto estimado se calcula como \(2\times \beta\).

Código

efectos1 <- c(mod1$coefficients[1], mod1$coefficients[-1]*2)
# efectos = coeficientes*2

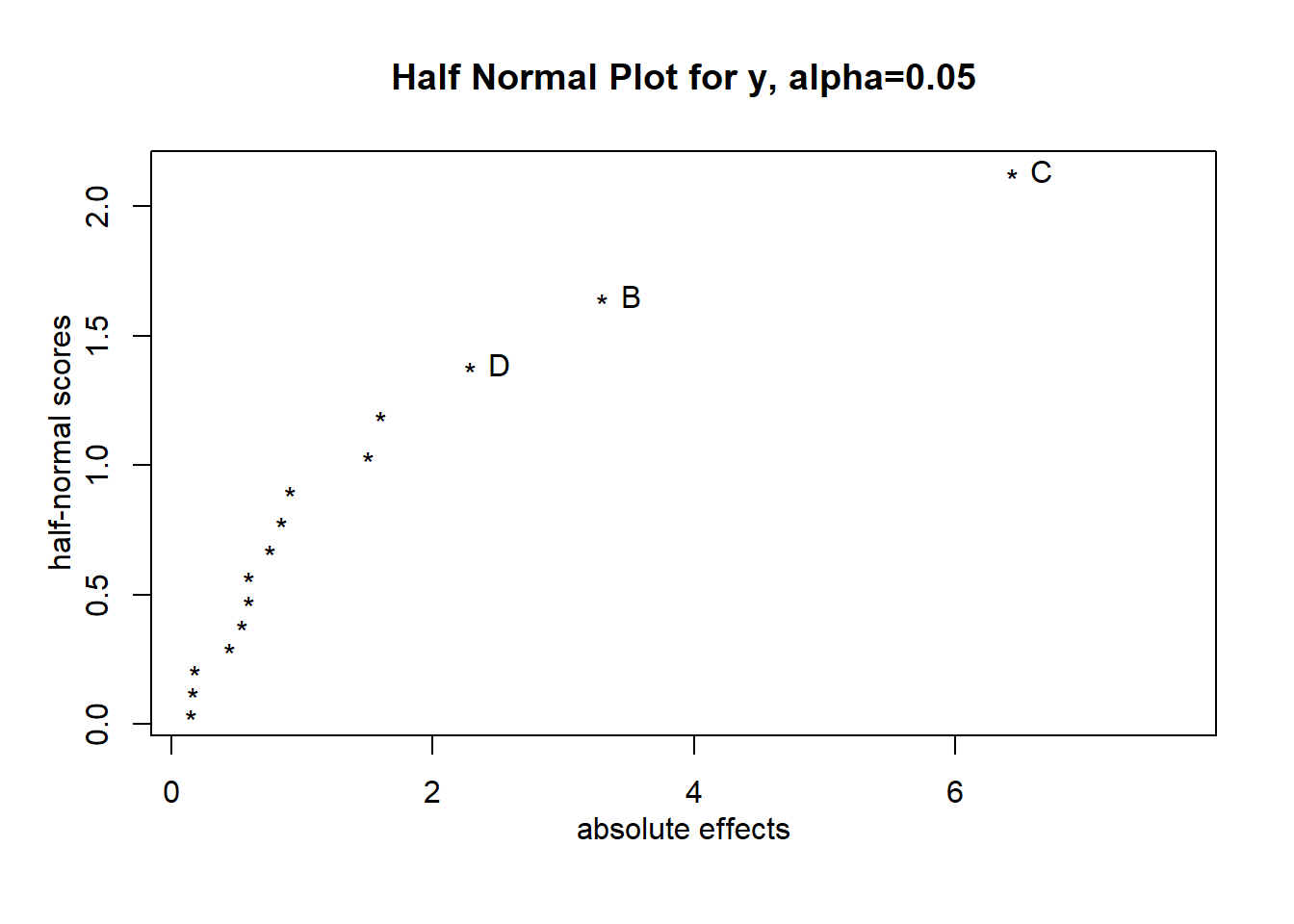
Dado que no es posible hacer un ANOVA, la significancia de los efectos puede ser aproximada por medio del Daniel Plot (half-normal plot), el cual identifica visualmente cuáles efectos son importantes (grandes).

Se calculan todos los efectos principales e interacciones
Se toma su valor absoluto
Se ordenan del más pequeño al más grande
Se grafican en un half-normal probability plot
- Eje x: estadísticas de orden esperadas de una distribución half-normal
- Eje Y: valores absolutos de los efectos

Código

DanielPlot(mod1, half = TRUE, alpha = 0.05)

El gráfico es una guía sobre la magnitud de los efectos, pero no representa un test formal de significancia estadística. En este caso, los efectos de los factores \(x_2 (B), x_3 (C)\) y \(x_4 (D)\) son identificados como importantes según el Daniel Plot. Las interacciones \(x_2x_3\) y \(x_3x_4\) también están un poco desviadas de los efectos que están alineados, pero no fueron marcados por el Daniel Plot como importantes.

12.1.2 Transformación Logarítmica

Se transforma la variable respuesta con logaritmo y se crea el diseño.

Código

lny <- log(y)
dis_lny <- add.response(dis, lny)
mod2 <- lm(lny ~ A*B*C*D, data=dis_lny)
summary(mod2)


Call:
lm.default(formula = lny ~ A * B * C * D, data = dis_lny)

Residuals:
ALL 16 residuals are 0: no residual degrees of freedom!

Coefficients:
             Estimate Std. Error t value Pr(>|t|)
(Intercept)  1.597728        NaN     NaN      NaN
A1           0.064995        NaN     NaN      NaN
B1           0.290041        NaN     NaN      NaN
C1           0.577226        NaN     NaN      NaN
D1           0.163271        NaN     NaN      NaN
A1:B1       -0.017182        NaN     NaN      NaN
A1:C1        0.005176        NaN     NaN      NaN
B1:C1       -0.025102        NaN     NaN      NaN
A1:D1        0.033450        NaN     NaN      NaN
B1:D1       -0.007469        NaN     NaN      NaN
C1:D1        0.049070        NaN     NaN      NaN
A1:B1:C1     0.005187        NaN     NaN      NaN
A1:B1:D1     0.026108        NaN     NaN      NaN
A1:C1:D1     0.026613        NaN     NaN      NaN
B1:C1:D1    -0.017256        NaN     NaN      NaN
A1:B1:C1:D1  0.019308        NaN     NaN      NaN

Residual standard error: NaN on 0 degrees of freedom
Multiple R-squared:      1, Adjusted R-squared:    NaN 
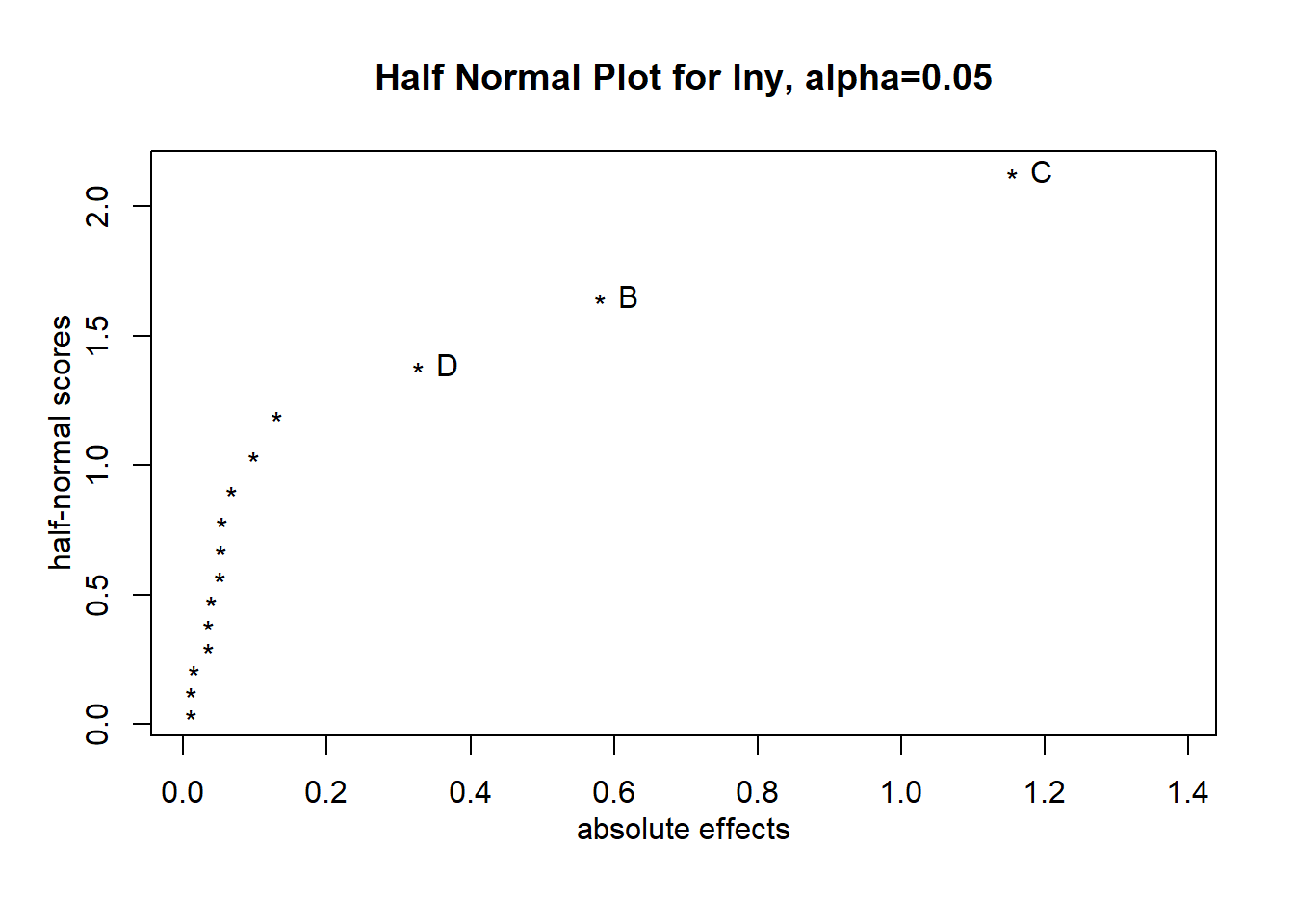
F-statistic:   NaN on 15 and 0 DF,  p-value: NA

Código

efectos2 <- c(mod2$coefficients[1], mod2$coefficients[-1]*2)

Código

DanielPlot(mod2, half = TRUE, alpha = 0.05)

El Daniel Plot sugiere que los factores importantes son \(x_2, x_3\) y \(x_4\).

Usando los factores sugeridos por el Daniel Plot, se ajusta el modelo y se hace el ANOVA, pues ahora sí hay grados de libertad para calcular el error residual.

Código

# Respuesta transformada - ln - Efectos seleccionados de acuerdo al Danielplot
mod3 <- lm(lny ~ B+C+D, data=dis_lny) 
summary(mod3)


Call:
lm.default(formula = lny ~ B + C + D, data = dis_lny)

Residuals:
      Min        1Q    Median        3Q       Max 
-0.166184 -0.073140  0.000175  0.052479  0.195711 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  1.59773    0.03006  53.143 1.30e-15 ***
B1           0.29004    0.03006   9.647 5.27e-07 ***
C1           0.57723    0.03006  19.200 2.25e-10 ***
D1           0.16327    0.03006   5.431 0.000152 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.1203 on 12 degrees of freedom
Multiple R-squared:  0.9762,    Adjusted R-squared:  0.9702 
F-statistic: 163.7 on 3 and 12 DF,  p-value: 5.339e-10

Código

(anova_mod <- aov(mod3))

Call:
   aov.default(formula = mod3)

Terms:
                       B        C        D Residuals
Sum of Squares  1.345979 5.331036 0.426521  0.173544
Deg. of Freedom        1        1        1        12

Residual standard error: 0.1202582
Estimated effects are balanced

Luego de ajustado el modelo de regresión, se obtuvo la siguiente ecuación de predicción:

\[\hat{y} = e^{1.5977 + 0.2900x_2 + 0.5772x_3 + 0.1633x_4}\]

A partir de esta ecuación, se obtienen las estimaciones de la media esperada de la variable respuesta para cada combinación de factores. Asimismo, se calcula el intervalo de confianza del \(95\%\) para cada estimación.

Código

# Matriz de diseño reducida y matriz especial
XRed <- model.matrix(mod3)
Mesp <- solve(t(XRed) %*% XRed)

# Parámetros para IC
sigma2 <- sigma(mod3)^2
t_crit <- qt(0.975, df = df.residual(mod3))

# Estimaciones y varianzas
estimates_log <- XRed %*% coef(mod3)
vars <- rowSums((XRed %*% Mesp) * XRed)

# IC en log y en escala original
se <- sqrt(sigma2 * vars)
ci_log <- cbind(
  Lower = estimates_log - t_crit * se,
  Estimate = estimates_log,
  Upper = estimates_log + t_crit * se
)

ci <- exp(ci_log)

# Resultados finales
results <- round(cbind(ci_log, ci), 2)
colnames(results) <- c("Lower_log","Estimate_log","Upper_log",
                       "Lower","Estimate","Upper")
results_log <- as.data.frame(results)

Código

flextable(results_log) %>%
  autofit() %>%
  set_header_labels(
    Lower_log = "Lower (log)",
    Estimate_log = "Estimate (log)",
    Upper_log = "Upper (log)",
    Lower = "Lower",
    Estimate = "Estimate",
    Upper = "Upper"
  ) %>%
  theme_vanilla() %>%
  align(align = "center", part = "all")

Tabla 1 - Intervalos de confianza (Modelo Log) en escala logarítmica y en escala original
Lower (log)	Estimate (log)	Upper (log)	Lower	Estimate	Upper
0.44	0.57	0.70	1.55	1.76	2.01
0.44	0.57	0.70	1.55	1.76	2.01
1.02	1.15	1.28	2.76	3.15	3.59
1.02	1.15	1.28	2.76	3.15	3.59
1.59	1.72	1.85	4.91	5.59	6.38
1.59	1.72	1.85	4.91	5.59	6.38
2.17	2.30	2.43	8.76	9.99	11.39
2.17	2.30	2.43	8.76	9.99	11.39
0.76	0.89	1.02	2.14	2.44	2.79
0.76	0.89	1.02	2.14	2.44	2.79
1.34	1.47	1.60	3.83	4.37	4.98
1.34	1.47	1.60	3.83	4.37	4.98
1.92	2.05	2.18	6.80	7.75	8.84
1.92	2.05	2.18	6.80	7.75	8.84
2.50	2.63	2.76	12.15	13.85	15.79
2.50	2.63	2.76	12.15	13.85	15.79

12.1.3 Modelo Lineal Generalizado

Se ajusta un Modelo Lineal Generalizado (MLG) asumiendo que la variable respuesta tiene una distribución Gamma, y se usa la función de enlace Logaritmo.

Código

# MLG - Modelo saturado
modg1 <- glm(y ~ A*B*C*D, data=dis_y, family = Gamma(link = "log"))

Warning in dgamma(y, 1/disp, scale = mu * disp, log = TRUE): Se han producido
NaNs

Código

summary(modg1)


Call:
glm(formula = y ~ A * B * C * D, family = Gamma(link = "log"), 
    data = dis_y)

Coefficients:
             Estimate Std. Error t value Pr(>|t|)
(Intercept)  1.597728        NaN     NaN      NaN
A1           0.064995        NaN     NaN      NaN
B1           0.290041        NaN     NaN      NaN
C1           0.577226        NaN     NaN      NaN
D1           0.163271        NaN     NaN      NaN
A1:B1       -0.017182        NaN     NaN      NaN
A1:C1        0.005176        NaN     NaN      NaN
B1:C1       -0.025102        NaN     NaN      NaN
A1:D1        0.033450        NaN     NaN      NaN
B1:D1       -0.007469        NaN     NaN      NaN
C1:D1        0.049070        NaN     NaN      NaN
A1:B1:C1     0.005187        NaN     NaN      NaN
A1:B1:D1     0.026108        NaN     NaN      NaN
A1:C1:D1     0.026613        NaN     NaN      NaN
B1:C1:D1    -0.017256        NaN     NaN      NaN
A1:B1:C1:D1  0.019308        NaN     NaN      NaN

(Dispersion parameter for Gamma family taken to be NaN)

    Null deviance:  7.0252e+00  on 15  degrees of freedom
Residual deviance: -5.4349e-16  on  0  degrees of freedom
AIC: NaN

Number of Fisher Scoring iterations: 1

Código

anova(modg1) # esto ya es un análisis de devianza

Analysis of Deviance Table

Model: Gamma, link: log

Response: y

Terms added sequentially (first to last)

        Df Deviance Resid. Df Resid. Dev
NULL                       15     7.0252
A        1   0.0882        14     6.9370
B        1   1.1967        13     5.7403
C        1   5.2109        12     0.5293
D        1   0.4241        11     0.1053
A:B      1   0.0047        10     0.1006
A:C      1   0.0006         9     0.1000
B:C      1   0.0093         8     0.0907
A:D      1   0.0177         7     0.0729
B:D      1   0.0009         6     0.0721
C:D      1   0.0387         5     0.0334
A:B:C    1   0.0004         4     0.0329
A:B:D    1   0.0109         3     0.0221
A:C:D    1   0.0113         2     0.0107
B:C:D    1   0.0048         1     0.0060
A:B:C:D  1   0.0060         0     0.0000

Código

efectos3 <- c(modg1$coefficients[1], modg1$coefficients[-1]*2)
sort(modg1$coefficients, TRUE)

 (Intercept)           C1           B1           D1           A1        C1:D1 
 1.597728288  0.577225902  0.290040837  0.163271482  0.064995204  0.049070479 
       A1:D1     A1:C1:D1     A1:B1:D1  A1:B1:C1:D1     A1:B1:C1        A1:C1 
 0.033450321  0.026613408  0.026108317  0.019308000  0.005186800  0.005175516 
       B1:D1        A1:B1     B1:C1:D1        B1:C1 
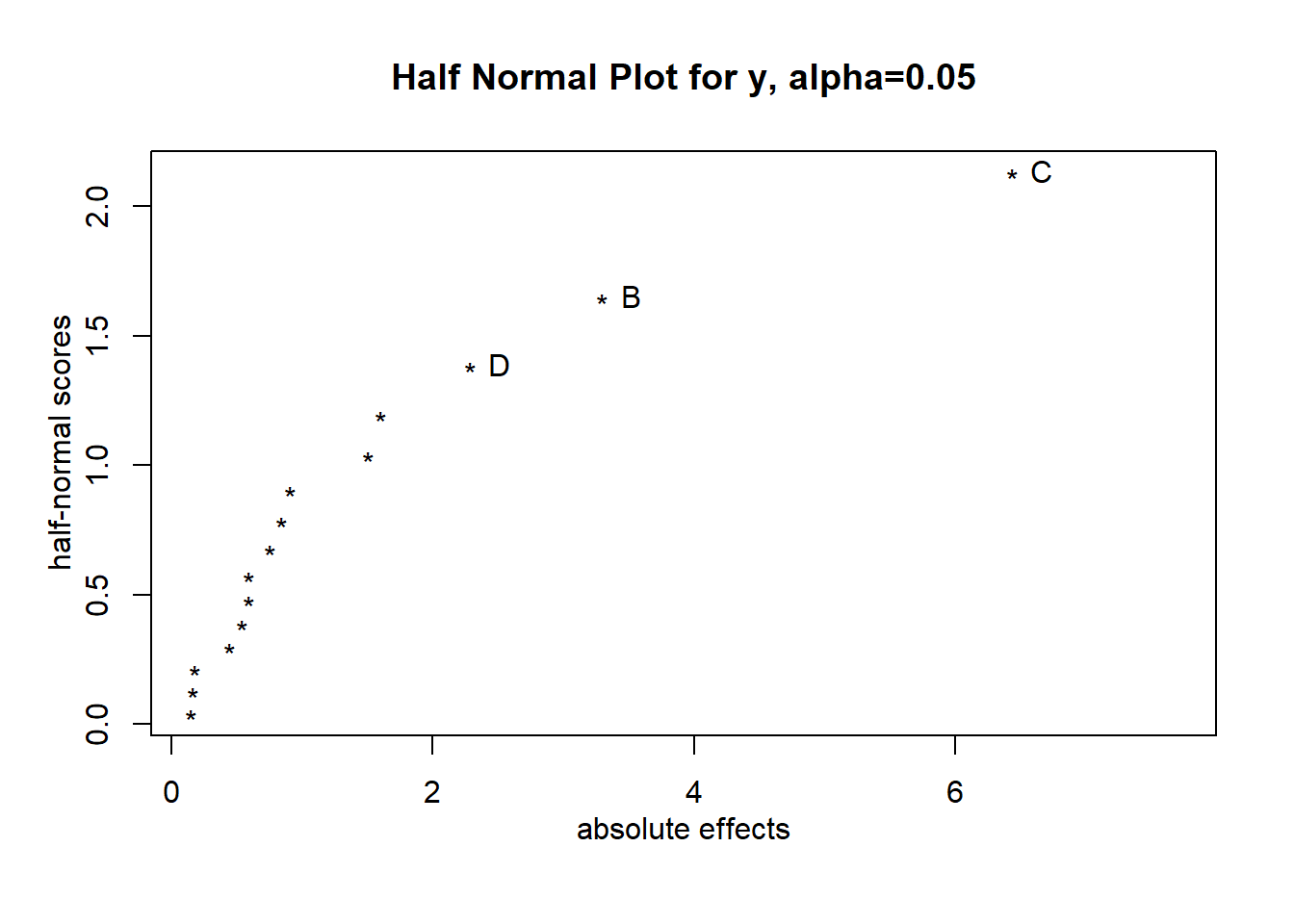
-0.007469293 -0.017181633 -0.017256294 -0.025102228

Código

DanielPlot(modg1, half = TRUE, alpha = 0.05)

En este caso, el Daniel Plot también sugiere que los factores más importantes son \(x1, x2\) y \(x3\).

Se ajusta entonces el modelo MLG usando los factores \(x_1, x_2\) y \(x_3\).

Código

modg2 <- glm(y ~ B+C+D, data=dis_y, family = Gamma(link = "log"))
summary(modg2)


Call:
glm(formula = y ~ B + C + D, family = Gamma(link = "log"), data = dis_y)

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  1.60317    0.03021  53.074 1.32e-15 ***
B1           0.28952    0.03021   9.585 5.65e-07 ***
C1           0.57894    0.03021  19.166 2.29e-10 ***
D1           0.16560    0.03021   5.482  0.00014 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

(Dispersion parameter for Gamma family taken to be 0.01459884)

    Null deviance: 7.02517  on 15  degrees of freedom
Residual deviance: 0.17404  on 12  degrees of freedom
AIC: 34.225

Number of Fisher Scoring iterations: 4

Código

anova(modg2)

Analysis of Deviance Table

Model: Gamma, link: log

Response: y

Terms added sequentially (first to last)

     Df Deviance Resid. Df Resid. Dev       F    Pr(>F)    
NULL                    15     7.0252                      
B     1   1.1914        14     5.8338  81.606 1.061e-06 ***
C     1   5.2241        13     0.6097 357.844 2.669e-10 ***
D     1   0.4357        12     0.1740  29.842 0.0001447 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

La ecuación de predicción obtenida en este caso es como sigue:

\[\hat{y} = e^{1.6032 + 0.2895x_2 + 0.5789x_3 + 0.1656x_4}\]

Los intervalos de confianza del \(95\%\) para la media condicional de las respuestas se calcularon mediante la fórmula de Wald para la distribución Gamma con enlace logarítmico, tal como se describe en Lewis (2001).

\[ e^{x_i' \hat{\beta}} \;\pm\; z_{\alpha/2} \, e^{x_i' \hat{\beta}} \, \nu \sqrt{\, x_i' (X'X)^{-1} x_i \,} \]

Código

X <- model.matrix(modg2)
eta_hat <- as.numeric(X %*% coef(modg2))
mu_hat  <- exp(eta_hat)        # keep full precision

M <- vcov(modg2)

se_eta <- sqrt(rowSums((X %*% M) * X))

z <- qnorm(0.975)

lower <- mu_hat - z * mu_hat * se_eta
upper <- mu_hat + z * mu_hat * se_eta

results_mlg <- data.frame(Lower    = as.numeric(lower),
                      Estimate = as.numeric(mu_hat),
                      Upper    = as.numeric(upper)) %>% 
  round(2)

Código

flextable(results_mlg) %>%
  autofit() %>%
  theme_vanilla() %>%
  align(align = "center", part = "all")

Tabla 2 - Intervalos de confianza (Modelo MLG)
Lower	Estimate	Upper
1.56	1.77	1.98
1.56	1.77	1.98
2.78	3.15	3.53
2.78	3.15	3.53
4.96	5.62	6.29
4.96	5.62	6.29
8.85	10.03	11.22
8.85	10.03	11.22
2.17	2.46	2.75
2.17	2.46	2.75
3.87	4.39	4.91
3.87	4.39	4.91
6.90	7.83	8.76
6.90	7.83	8.76
12.32	13.97	15.63
12.32	13.97	15.63

12.1.4 Resultados

A continuación se muestran los efectos estimados del modelo saturado usando los tres modelos: MCO con los datos originales, MCO con los datos transformados con logaritmo y el modelo MLG.

Código

# Nombres de los efectos
efectos_nombres <- c(
  "Intercepto", 
  "x1", "x2", "x3", "x4",
  "x1:x2", "x1:x3", "x2:x3", "x1:x4", "x2:x4", "x3:x4", 
  "x1:x2:x3", "x1:x2:x4", "x1:x3:x4", "x2:x3:x4",
  "x1:x2:x3:x4"
)

tabla_efectos <- data.frame(
  Efecto = efectos_nombres,
  Efectos1 = round(efectos1, 3),
  Efectos2 = round(efectos2, 3),
  Efectos3 = round(efectos3, 3)
)

Código

flextable(tabla_efectos) %>%
  autofit() %>%
  set_header_labels(
    Efecto = "Efecto",
    Efectos1 = "Datos originales",
    Efectos2 = "Transformación log",
    Efectos3 = "MLG"
  )

Tabla 3 - Efectos estimados: MCO datos originales, MCO datos transformados y MLG
Efecto	Datos originales	Transformación log	MLG
Intercepto	6.155	1.598	1.598
x1	0.912	0.130	0.130
x2	3.298	0.580	0.580
x3	6.433	1.154	1.154
x4	2.285	0.327	0.327
x1:x2	0.150	-0.034	-0.034
x1:x3	0.595	0.010	0.010
x2:x3	1.505	-0.050	-0.050
x1:x4	0.843	0.067	0.067
x2:x4	0.442	-0.015	-0.015
x3:x4	1.598	0.098	0.098
x1:x2:x3	0.167	0.010	0.010
x1:x2:x4	0.590	0.052	0.052
x1:x3:x4	0.755	0.053	0.053
x2:x3:x4	0.180	-0.035	-0.035
x1:x2:x3:x4	0.537	0.039	0.039

Los efectos estimados obtenidos con el modelo MCO con los datos transformados y el modelo MLG son los mismos.

Para evaluar la precisión de las estimaciones del modelo, puede analizarse la amplitud de los intervalos de confianza. Una menor amplitud indica mayor precisión en las estimaciones, mientras que intervalos más amplios reflejan mayor incertidumbre.

Código

amp_log <- results_log$Upper - results_log$Lower
amp_mlg <- results_mlg$Upper - results_mlg$Lower

amplitudes <- data.frame(
  Amplitud_Log = amp_log,
  Amplitud_MLG = amp_mlg
)

Código

flextable(amplitudes) %>%
  autofit() %>%
  theme_vanilla() %>%
  align(align = "center", part = "all")

Tabla 4 - Amplitud de los intervalos de confianza al 95%
Amplitud_Log	Amplitud_MLG
0.46	0.42
0.46	0.42
0.83	0.75
0.83	0.75
1.47	1.33
1.47	1.33
2.63	2.37
2.63	2.37
0.65	0.58
0.65	0.58
1.15	1.04
1.15	1.04
2.04	1.86
2.04	1.86
3.64	3.31
3.64	3.31

Se observa que la amplitud de los intervalos de confianza de las estimaciones obtenidas con el modelo MLG es menor que la del modelo MCO con transformación logarítmica, lo que refleja una mayor precisión en la estimación de la media.

Volver arriba